はじめに
前回の記事では,ADCの性能を示すための重要な指標である SQNR と ENOB について学びました.量子化によって信号がどれだけ劣化するのかを数値で表すこの指標は,ADC性能の根幹をなす重要な要素です.
今回はそのSQNRの式をもう一度振り返りながら,「6.02」と「1.76」という数字がどこから現れるのかを丁寧に導出していきます.
これらはマジックナンバーではなく,波形の平均電力から自然に導かれるものです.
それでは,ENOBの式がどのように形づくられるのかを見ていきましょう.
SQNRの復習
SQNR(Signal to Quantization Noise Ratio)は,信号パワー(\(P_S\)) ÷ 雑音パワー(\(P_Q\)) で定義される指標でしたね.
\(\mathrm{SQNR} = \frac{P_S}{P_Q}\)
したがって,まず「信号パワー」と「雑音パワー」をそれぞれ正しく算出する必要があります.
このときの信号パワーは入力波形の 平均電力(time-average power) であり,時間方向に積分して求めます.「どの波形を,どの範囲で積分して平均化するか」によって,最終的なSQNRの定数項が決まるわけです.
では,順番に解いていきましょう.
信号パワー(平均電力)の導出
信号パワーを示す平均電力とは,波形の瞬時電力 \(x^2(t)\) を時間方向に積分して得られる面積の平均です.この平均値が波形全体のエネルギー密度を表し,RMS(Root Mean Square)値の2乗としても理解できます.
\(P_S = \frac{1}{T}\int_0^T x^2(t)\,dt\)
まずは最も一般的な正弦波入力を考えます.周期 \(T=1/f\),振幅 \(A=V_{\mathrm{ref}}\) とします.
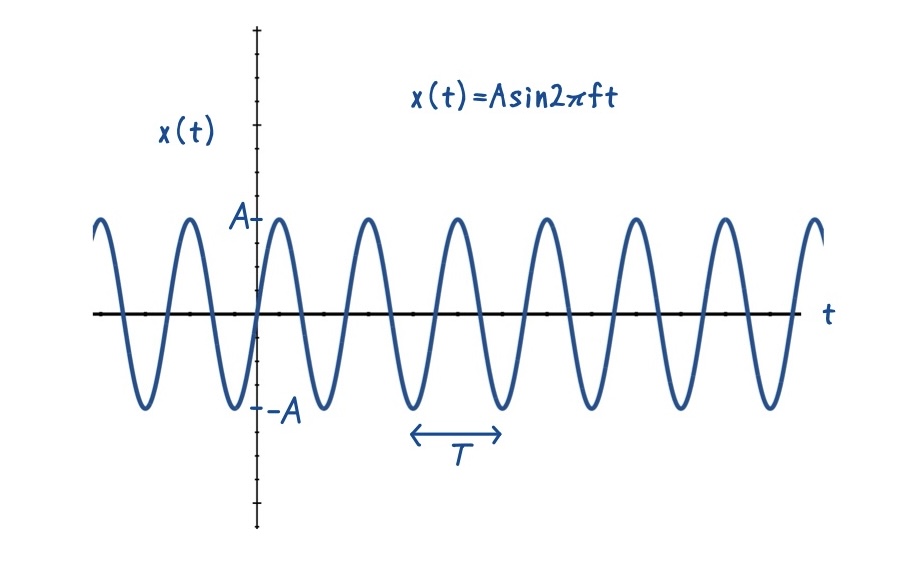
振幅が \(V_{\mathrm{ref}}\) なのは,ADCの入力フルスケールに対応していましたね.
したがって,1ステップあたりの電圧は \(\Delta = 2V_{\mathrm{ref}}/2^N\) です(前々回の記事の復習).
\(x(t) = A\sin(2\pi f t)\)
1周期あたりの平均電力は \(x^2(t)\) の積分値の平均で求められます.
\(P_S = \frac{1}{T}\int_0^T A^2\sin^2(2\pi f t)\,dt = \frac{A^2}{2}\)
展開も確認しておきましょう(あえて位相軸ではなく,時間軸で計算しています).
\(\begin{aligned} P_s &= \frac{A^2}{T} \int_0^T \frac{1-\cos(4\pi f t)}{2}\,dt\\ &= \frac{A^2}{T}\left[\frac{t}{2} – \frac{\sin(4\pi f t)}{8\pi f}\right]_0^T = \frac{A^2}{2} \end{aligned}\)
ここで,\(A=V_{\mathrm{ref}}\) とすると,
\(P_S = \frac{V_{\mathrm{ref}}^2}{2}\)
これで信号パワーを求めることができました.
ちなみに実効値(RMS値)はその平方根で \(V_{\mathrm{ref}}/\sqrt{2}\) です.
波の実行値や平均値,平均電力はよく使うので,頭に染み付いている人は多いと思います.
特にこの業界では.知っていて当たり前のように使われるので,覚えておいて損はありません.
毎回導出したり調べたりするのは大変ですもんね.
雑音パワー(平均電力)の導出
雑音パワーも同様に平均電力として導出します.
量子化雑音の解析には,
- 確率論モデル(誤差が一様分布)
- 決定論モデル(実際の時間波形を積分)の2つのアプローチがあります.
前々回の記事では「一様分布の確率モデル」から,雑音パワー \(P_Q = \Delta^2/12\) を導出しました.
今回は信号パワーと対比させるために,時間波形から雑音パワーを求めます.
結果としてはもちろん同じく \(\Delta^2/12\) になります.
下図に,入力信号と量子化された出力信号,そしてその差分の量子化誤差を示します.
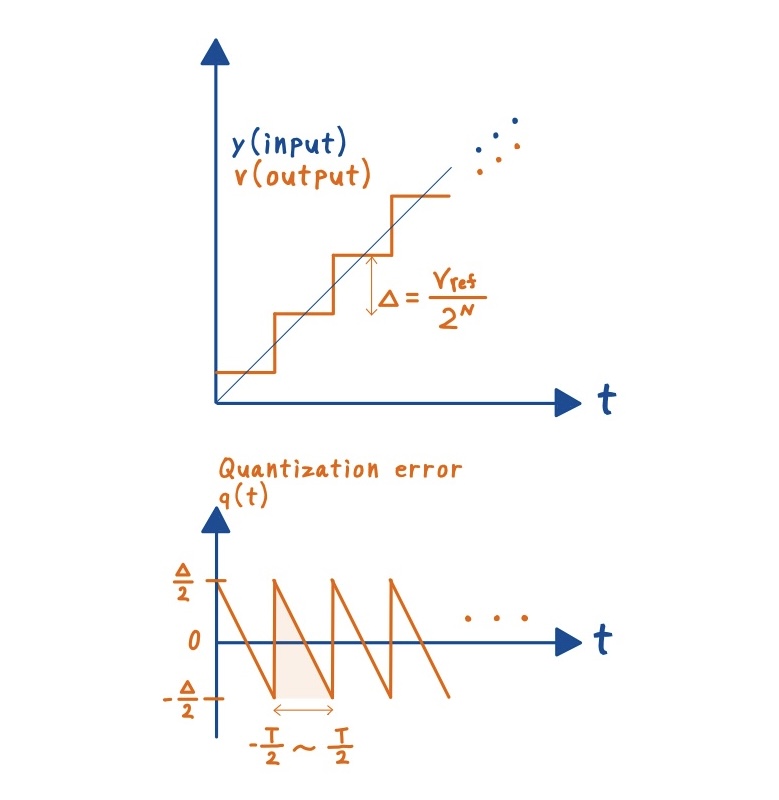
量子化によって出力は階段状になり,量子化誤差は鋸状の波形になります.1周期の間でΔステップずつ登るイメージです.
ここで「信号パワーは正弦波で導出するのに,雑音パワーの入力信号はランプ波形でいいのか?」という疑問が湧くかもしれません.
結論としては,ビット数が大きければ十分近似できるため,いずれの波形を用いても最終結果は一致します.
どうしても正弦波で確認したい方は,付録をご覧ください(筆者もその一人でした).
大変な導出になるので,「どんな波形でも,高分解能なら平均雑音パワーはほぼ同じ値に近似できる」と考えてOKです.
量子化誤差を \(q(t)\) とすると,雑音パワーは次式です.
\(P_Q = \frac{1}{T}\int_{-T/2}^{T/2} q(t)^2\,dt\)
周期ごとに同じ誤差波形が繰り返されるため,1周期のみを積分しても結果は変わりません.
区間 [-T/2, T/2] において,ランプ波形状の誤差は
\(q(t) = \frac{\Delta}{T}t\)
と表されます(誤差が ±Δ/2 の範囲で線形に増減すると仮定).
これを代入すると,
\(\begin{aligned} P_Q &= \frac{1}{T}\int_{-T/2}^{T/2} \left(\frac{\Delta t}{T}\right)^2\,dt = \frac{\Delta^2}{T^3}\int_{-T/2}^{T/2} t^2\,dt\\ &= \frac{\Delta^2}{T^3}\left[\frac{t^3}{3}\right]_{-T/2}^{T/2} = \frac{\Delta^2}{12} \end{aligned}\)
以上から,雑音パワーは \(\Delta^2/12\) になります.
確率論モデルから導いたときの結果と完全に一致しましたね.
ここまでで,SQNRの算出に必要な信号パワー \(P_S\) と雑音パワー \(P_Q\) が揃いました.
ENOBの導出
「6.02」と「1.76」がどこから出てきたのかを確かめましょう.
最終的には\(P_S\)と\(P_Q\)の比を求めるのですが、SNRは通常「デシベル(dB)」で表します。
デシベルは比を対数で表したもので,
\(\mathrm{SNR_{dB}} = 10\log_{10}\!\left(\frac{P_S}{P_Q}\right)\)
と定義されます.これによって非常に大きな比を扱いやすいスケールに変換できます.
\(\begin{aligned} \mathrm{SNR} &= 10\log_{10}\frac{P_S}{P_Q} = 10\log_{10}\frac{V_{\mathrm{ref}}^2/2}{\Delta^2/12}\\ \end{aligned}\)
ここで \(\Delta = 2V_{\mathrm{ref}}/2^N\) を代入します.
\(\begin{aligned} \mathrm{SNR} &= 10\log_{10}\left(\frac{3}{2}\right) + N・10\log_{10}2^2 = 1.76 + 6.02N \end{aligned}\)
これで SNR=6.02 N + 1.76 dB が導けました.
この式を逆にして N を求めたものが ENOB です.SNR式は理想ビット数Nに対する理論値を表しているため,実測のSNRを代入してNを逆算すれば,実際のADCの有効ビット数が求められるということです.
\(\mathrm{ENOB} = \frac{\mathrm{SNR} – 1.76}{6.02}\)
ここで SQNRではなく,あえてSNR と書いているのは,実測では量子化雑音以外の成分も含まれるためです.実測やシミュレーションで得られる SNR は,環境ノイズや歪みなど量子化以外の成分を含むため,より一般的には SNR や SINAD(Signal-to-Noise-and-Distortion) を用いて評価します.
→ 参考: Analog Devices – ENOBの求め方
まとめ
- 正弦波の信号パワーは\(P_S = \frac{V_{\mathrm{ref}}^2}{2}\)
(ちなみにランプ波の信号パワーは \(\frac{V_{\mathrm{ref}}^2}{3}\).→ この違いが「+1.76 dB」の差を生む.) - 雑音パワーは\(P_Q=\Delta^2/12\)
- 6.02 は対数の傾き \(20\log_{10}2\) に由来する.
- 1.76 は信号波形の平均電力比 \(10\log_{10}(3/2)\) に由来する.
- ENOB は理想 SNR 式を逆に用い,実測性能を理想ビット換算で表したもの.
以上,最後まで読んでいただきありがとうございました.
正弦波を入力にしたときの雑音パワーを導出したい方は付録をご参照ください.筆者の疑問解消のため,せっかく解いたので載せておきます.
次回は離散時間フーリエ変換→離散フーリエ変換の関係を整理し,サンプリング信号を周波数領域でどう理解するかをまとめていきます.
参考文献
本記事はあくまで筆者の勉強備忘録のため,より正確に理解したい,さらに深く理解したい場合は下記をご参照ください.
- IIT Kanpur: https://www.iitk.ac.in
- SSCD Lab: https://iitk.ac.in/sscd
- 講義動画(YouTube): https://youtu.be/cI7bYpW7EvE?si=uhuL8tSMJan23LHf
- 『アナログ/デジタル変換入門 ― 原理と回路実装 ―』 和保孝夫(監)/コロナ社
https://www.coronasha.co.jp/np/isbn/9784339009187 - 『ΔΣ型アナログ/デジタル変換器入門 第2版』 和保孝夫・安田彰(監訳)/丸善出版
https://www.maruzen-publishing.co.jp/book/b10120696.html
今回解説した内容は下記講義動画を参考にしています.
付録:雑音パワーを正弦波から導出(マニア向け)
ここに、先ほど話題にした「正弦波入力から直接 Δ²/12 を導く」を詳述します。


コメント