はじめに
これまでの記事では，ADCの性能指標である SQNR（Signal-to-Quantization Noise Ratio） や ENOB（Effective Number of Bits） について学びました．これらはいずれも，信号を周波数領域で評価する指標でしたね．
今回は，ADCのもうひとつの重要な側面――非線形性（nonlinearity） について解説します．これまでは理想的なADCを仮定していましたが，実際のADCは，内部のコンパレータや基準電圧源のばらつきによって，わずかな非線形性（直線からの歪み）を持ちます．この非線形性を定量的に表す代表的な指標が，DNL（Differential Nonlinearity） と INL（Integral Nonlinearity） です．
本稿では，これらの意味と違いを丁寧に整理し，データシートに記載されている「DNL ±0.5 LSB」などの数値が何を意味するのかを，直感的に理解できるようになることを目指します．
量子化器復習
まずは基準となる「理想的な量子化器（Ideal Quantizer）」を復習しておきましょう．
以前の記事でも触れたように，例として 入力範囲を −1V〜+1V，出力レベルを 8 段階（3bit）に分けるADC を考えます．このとき，理想的なステップ幅（1 LSB：Least Significant Bit）は次のように表されます．
\(\Delta = \frac{V_\text{FS+} – V_\text{FS−}}{2^N} = \frac{2}{8} = 0.25\,\text{V}\)
1コード分の入力電圧幅は 0.25V で，各コードの境界（遷移電圧 \(V_k\)：transition voltage）は… ,-0.5, -0.25, 0, 0.25, -0.5 … のように等間隔に並びます．
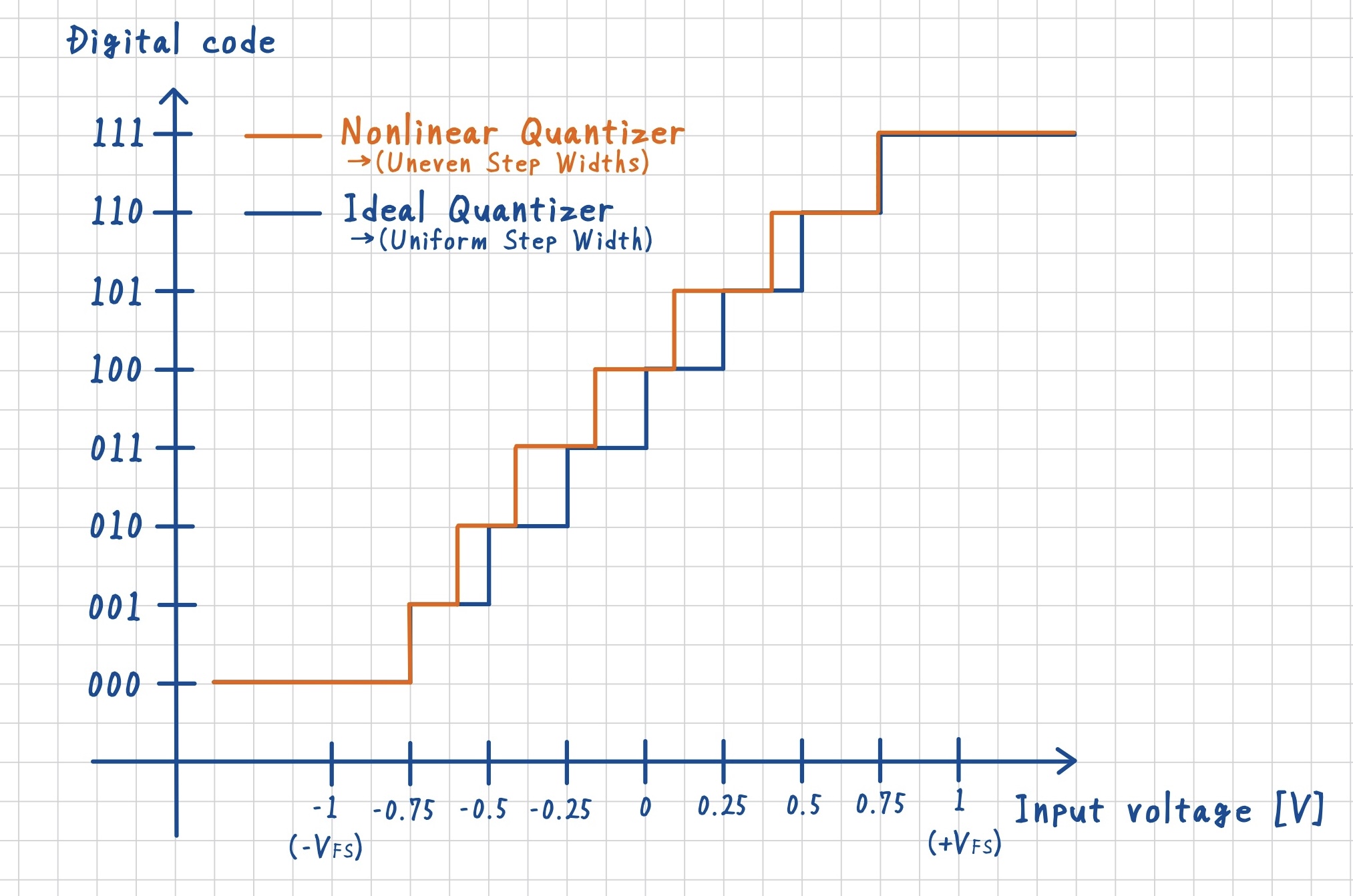
このとき，入力電圧に対する出力コードの特性をグラフにすると階段状ではあるものの，各ステップの幅がすべて等しいため，全体としては一本の直線のように見えます．この状態を「線形量子化器（linear quantizer）」と呼びます．
言い換えると，「入力電圧が一定量変化するごとに出力コードも同じ量だけ進む」という関係が保たれているということです．
このような理想的な量子化器であれば，入力にサイン波を与えた場合でも，出力の周波数特性にはサイン波成分と量子化雑音しか現れず，高調波（harmonics）は発生しません．これは，量子化特性が等間隔で非線形成分を含まないためです．
図1：理想的な量子化特性（全コード幅が等しい）
非線形な量子化器とは？
実際のADCでは，コンパレータのしきい値や基準電圧源のばらつき，配線抵抗や素子ミスマッチなどの影響によって，各ステップ幅 \(\Delta_k\) が完全に均一ではなくなることがあります．
この場合，遷移電圧を結んだ線は理想的な直線からわずかにずれ，下図のように歪んだカーブになります．
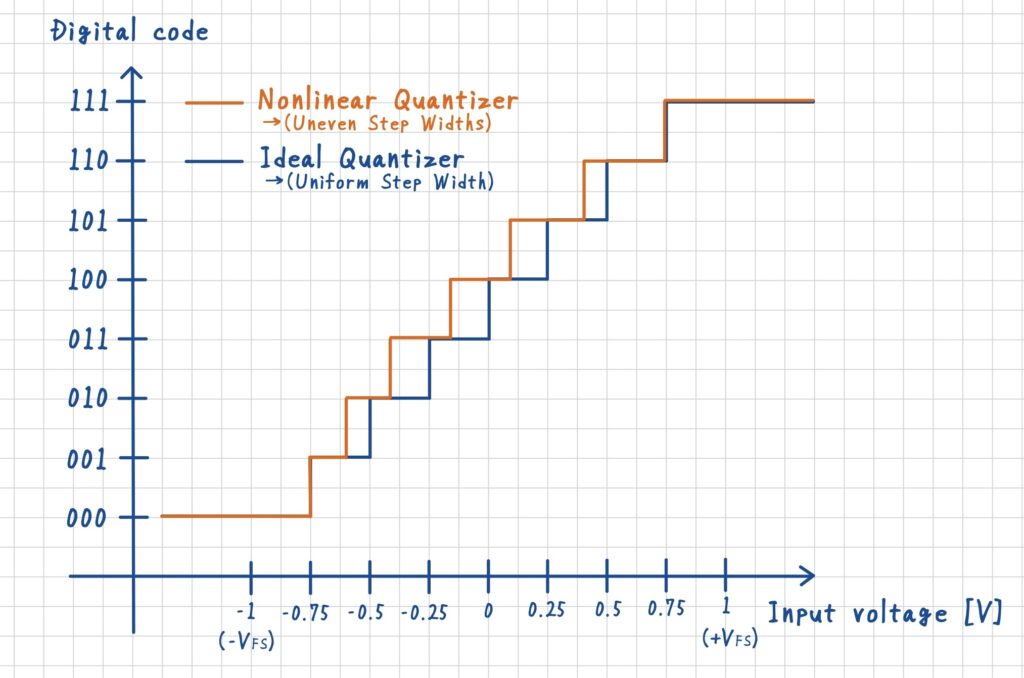
このように遷移点が不均一なADCにサイン波を入力すると，理想的な場合には現れなかった高調波成分（harmonics）が出力スペクトルに現れます．これは，入力と出力の関係が等間隔ではなくなり，局所的に非線形な写像となることで，サイン波が他の周波数成分へと“折り曲げられる”ためです．
この“歪み”こそが 非線形性（nonlinearity） であり，後で示す DNL（Differential Nonlinearity） および INL（Integral Nonlinearity） によって定量的に表すことができます．
ここで注意すべき点としては，「非理想」＝「非線形」ではないということです．
下記のズレ(後の章で解説)は，線形誤差（linear error） と呼ばれ，非線形性には含まれません．すなわち，波形歪みやharmonicsの原因にはならないということです．
- ゲイン誤差（Gain Error）：すべてのステップ幅は等しいが，理想値より大きい／小さい
- オフセット誤差（Offset Error）：すべてのコードが一定量だけ上下にシフトしている
DNLとINL ― 非線形性を定量化する指標
DNL（Differential Nonlinearity：微分非直線性）
DNLは，各コード幅が理想値からどれだけズレているかを表す指標で，定義式は次のとおりです．
\(\mathrm{DNL}(k) = \frac{\Delta_k – \Delta_\mathrm{ideal}}{\Delta_\mathrm{ideal}}\)
- \(\Delta_k\)：コード k の実際の幅
- \(\Delta_\mathrm{ideal}\)：理想ステップ幅（通常は平均ステップ幅 \(\Delta_\mathrm{avg}）\)
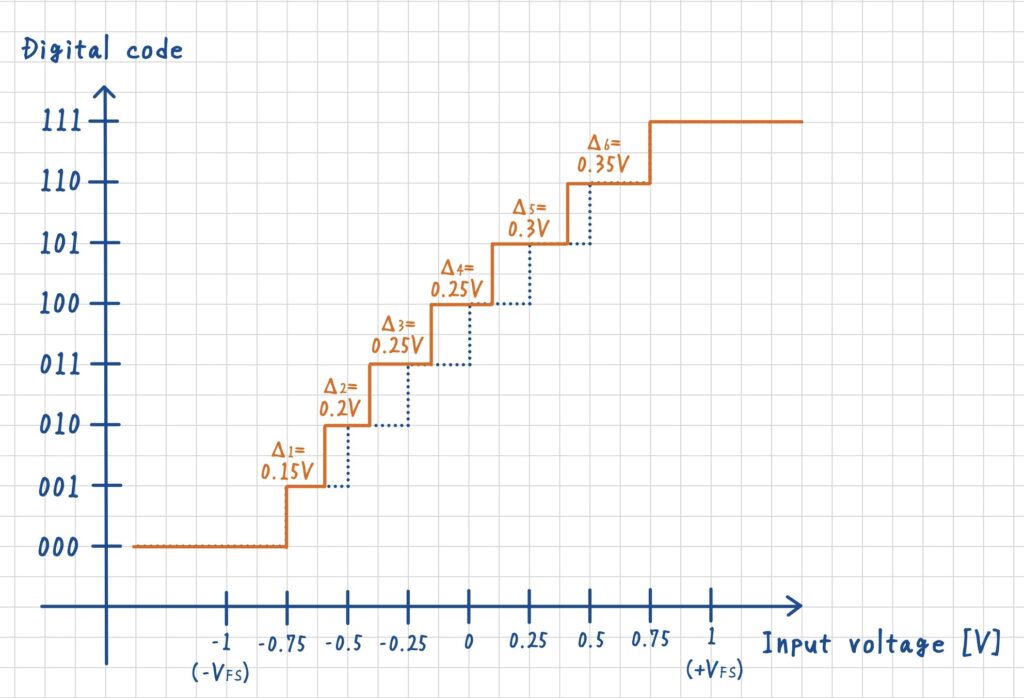
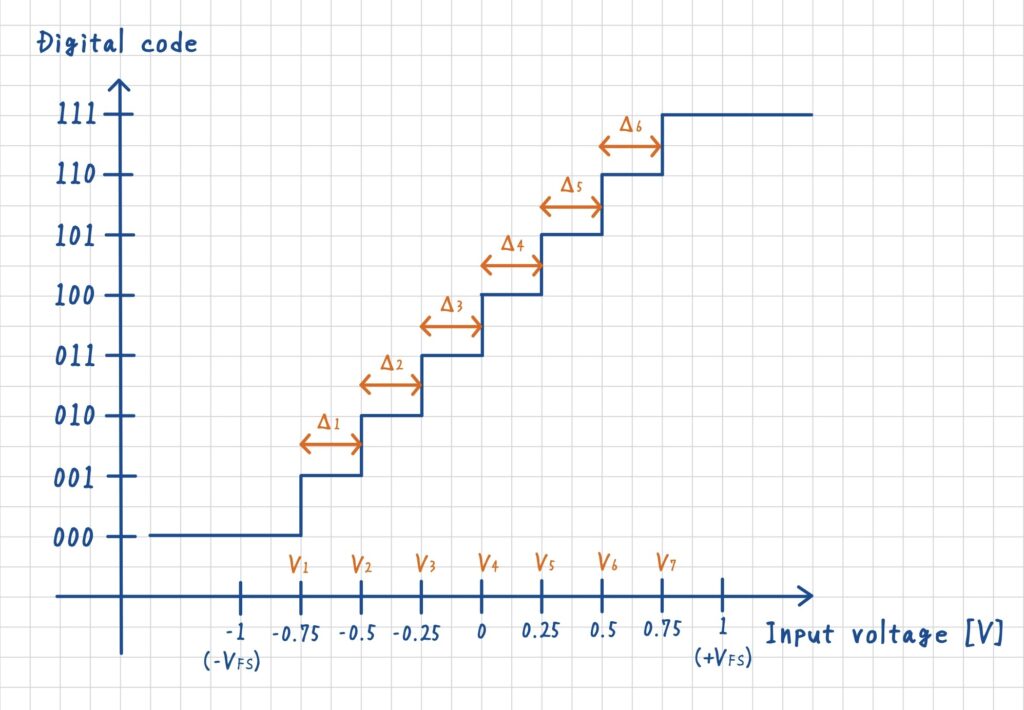
下表に，非線形な量子化器における DNL の算出例を示します．両端のコードに対応する DNL は定義できません．理由として，端のステップ幅 \(\Delta_0\) および \(\Delta_7\) は入力範囲が無限に続くため，理論的に幅が決まらないからです．
したがって，今回の例では DNL(0) および DNL(7) は未定義となります．
| k | Δ_k [V] | DNL(k) [LSB] |
|---|---|---|
| 0 | – | – |
| 1 | 0.15 | −0.4 |
| 2 | 0.20 | −0.2 |
| 3 | 0.25 | 0 |
| 4 | 0.25 | 0 |
| 5 | 0.30 | +0.2 |
| 6 | 0.35 | +0.4 |
| 7 | – | – |
もし DNL が 0 LSBであれば，そのコード幅は理想的であることを意味します．(今回の例では，DNL(3),DNL(4))
一方で，DNL = −1 の場合，そのステップは 存在しない（missing code） 状態になります．この理由を下図を用いて説明します．
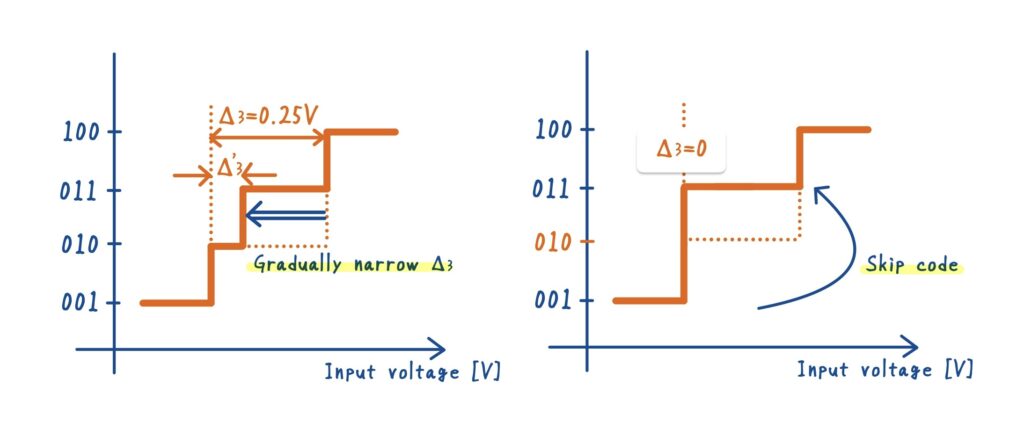
今，あるステップ幅が \(\Delta_3 = 0.25\,\mathrm{V}\) であったとします．この \(\Delta_3\) を徐々に小さくしていくと，やがて \(\Delta_{3,\mathrm{min}} = 0\) に達します．このとき，DNL の定義式に代入すると次のようになります．
\(\mathrm{DNL}(3) = \frac{0 – \Delta_\mathrm{ideal}}{\Delta_\mathrm{ideal}} = -1\)
これは「そのステップ幅が完全に潰れた」ことを意味します．このとき出力コード「010」が消滅し，「001」から「011」へと一気にジャンプします．
したがって，ADC における DNL の性能としては，missing code が発生しない条件として次が必須となります．
\(-1 < \mathrm{DNL}(k) < +1\)
まとめると，DNL は，「1ステップごとの“階段の均一さ”を測る指標」であり，局所的な量子化誤差の歪みを直接的に反映する，非常に実務的なパラメータです．
INL（Integral Nonlinearity：積分非直線性）
次にINLです．INLは、量子化特性全体が理想直線からどれだけ離れているかを表す指標で，定義式は次のとおりです．
\(\mathrm{INL}(k) = \frac{V_k – V_{k,\mathrm{ideal}}}{\Delta_\mathrm{ref}}\)
- \(V_k\)：実際の遷移電圧
- \(V_{k,\mathrm{ideal}}\)：理想直線上の遷移電圧
- \(\Delta_\mathrm{ref}\)：基準となるステップ幅（通常は \(\Delta_\mathrm{ideal}\) または \(\Delta_\mathrm{avg}）\)
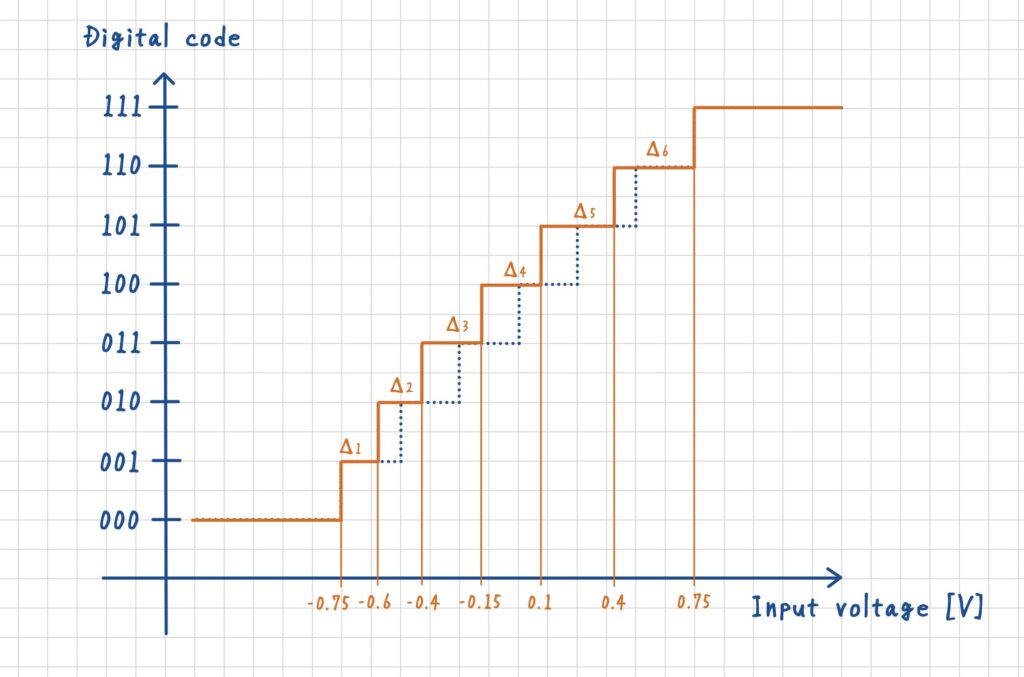
下表は，上図に対応する非線形な量子化器におけるINLの算出です．
| k | V_k [V] | V_{k,\mathrm{ideal}} [V] | INL(k) [LSB] |
|---|---|---|---|
| 1 | −0.75 | −0.75 | 0.0 |
| 2 | −0.60 | −0.50 | −0.4 |
| 3 | −0.40 | −0.25 | −0.6 |
| 4 | −0.15 | 0.00 | −0.6 |
| 5 | +0.10 | +0.25 | −0.6 |
| 6 | +0.40 | +0.50 | −0.4 |
| 7 | +0.75 | +0.75 | 0.0 |
一般的にADCでは，INL(0) は定義されません．これは，最初の遷移点 \(V_0\) が入力範囲の外側（−∞ から最初のコード境界まで）を表すため，理想直線上に対応する比較点が存在しないからです．
一方で，INL(1) と INL(7) は端点を基準とした理想直線と一致しているため 0 になります．INLが負方向に続いていることから，全体として特性がやや圧縮された形になっていることが分かります．
今回の例では端点がすでに理想と揃っていましたが，端点がずれている場合には，補正によって端点を一致させる必要があります．これが，後程解説するゲイン誤差やオフセット誤差の補正です．これらは線形的な誤差のため，INLの形状そのものには影響しません．
補正を行なった場合は，単純に \(\Delta_\mathrm{ideal}\) を使うのではなく，実際のフルスケール範囲を \(2^N\) で割って求めた平均ステップ幅 \(\Delta_\mathrm{avg}\) を基準として計算するのが一般的です．
補足ですが，INLの定義には大きく分けて エンドポイント法（end-point fit） と ベストフィット法（best-fit line） の2種類があります．今回の例はエンドポイント法に対応しており，端点を理想直線に固定してINLを算出しています．ベストフィット法は，全データ点に対して最小二乗法で求めた「平均的に最も近い直線」を基準とする定義です．
(筆者自身の実務経験としては，エンドポイント法しか使用したことがなく，ベストフィット法を採用するケースをあまり知りません．)
まとめると，INLは次のように整理できます．
量子化特性全体の「曲がり具合」を示す指標であり，INLが小さいほど，ADCはより理想的な直線に近づきます．
DNLとINLの関係
ここまでの説明でお気づきかもしれませんが，DNLとINLはお互いに独立した指標ではなく，次のような関係で結ばれています．
\(\mathrm{INL}(k+1) – \mathrm{INL}(k) = \mathrm{DNL}(k)\)
DNLを積み上げるとINLになり，逆にINLを差分（隣り合う点の差）を取るとDNLになるという関係です．直感的に言えば，DNLは「局所的なズレ」を，INLは「全体として積み上がったズレ」を示しています．
下表は，これまでの章で扱った3bit ADCの例をまとめたものです．上式の関係が，実際に各コード間で成り立っていることが分かります．
| k | DNL(k) [LSB] | INL(k) [LSB] |
|---|---|---|
| 0 | – | – |
| 1 | −0.4 | 0 |
| 2 | −0.2 | −0.4 |
| 3 | 0 | −0.6 |
| 4 | 0 | −0.6 |
| 5 | +0.2 | −0.6 |
| 6 | +0.4 | −0.4 |
| 7 | – | 0 |
今回の例では，理解を優先するために講義でも取り扱った3bitの簡素なADCで説明しましたが，実際のADCでは，DNL/INLは下図に示すようにより複雑な形状を示します．特に2進数で重みづけしたような回路構成の場合，DNL/INLはビットの切り替わりポイントで局所的に誤差が大きくなることがよくあります．
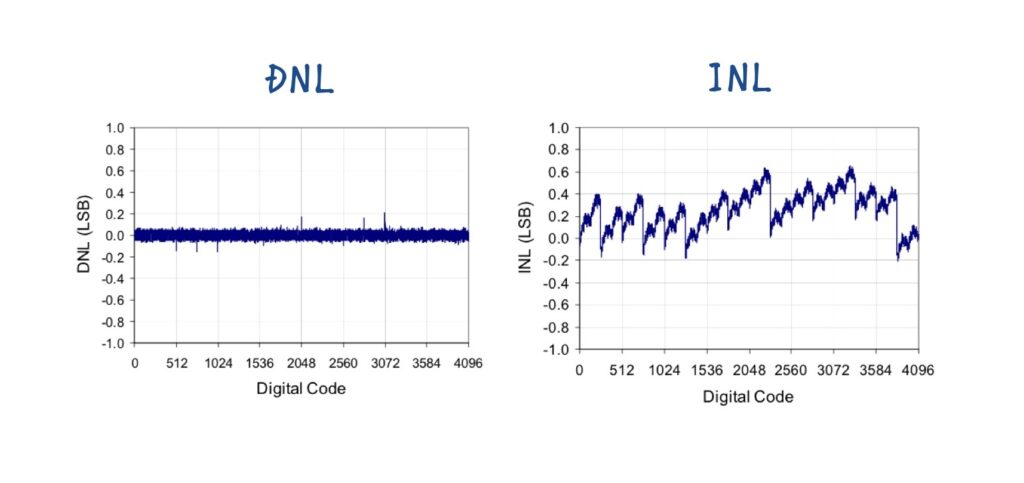
https://ww1.microchip.com/downloads/jp/AppNotes/00693A_JP.pdf
引用先:Microchip Technology Inc.
線形成分（ゲイン誤差・オフセット誤差）の扱い
現実のADCでは、非線形性だけでなく，必ずと言っていいほど線形誤差も存在します．
まずはこれらを理解し，評価から分離しておくことが重要です．
誤差（Gain Error）
すべてのコード幅が一定であっても，それが理想の \(\Delta_\mathrm{ideal}\) よりわずかに大きい／小さい場合，全体の傾き（slope）が変化します．
これは，特性全体が「直線のまま伸び縮みしている」だけの状態であり，入力と出力の比例関係は保たれているため非線形ではありません．したがって，このような場合にDNLを計算する際は，理想値 \(\Delta_\mathrm{ideal}\) の代わりに実際の端点を基準として求めた平均ステップ幅 \(\Delta_\mathrm{avg}\) を用いることで，傾きの違いを補正します．
\(\Delta_\mathrm{avg} = \frac{V_{T,\max} – V_{T,\min}}{2^N}\)
この補正によって，ゲイン誤差は除去され，DNLやINLが純粋に非線形性のみを反映するようになります．
オフセット誤差（Offset Error）
オフセット誤差は，特性全体が一定量だけ上下に平行移動している状態を指します．すべての遷移電圧に同じ値が加算されているだけなので，曲線の形状やステップ幅自体は変化していません．
このため，INLやDNLの形状には影響しませんが，正しい基準線（理想直線）を定めるために，評価前にこのオフセットを取り除く必要があります．
実際の解析では，最初に遷移電圧データの平均や端点を参照してオフセット量を求め，その分を引き算してからINLを計算します．
まとめると，
- ゲイン誤差：傾きの違い → Δavgで補正
- オフセット誤差：上下のズレ → 平行移動で補正
どちらも「線形誤差」であり，非線形性（DNL／INL）とは区別して扱うことが重要です．
実務での測定・評価手順
実際にADCの非線形性（DNL／INL）を測定・評価する場合，以下の手順で解析を行うのが一般的です．
① 遷移電圧の全測定
入力電圧をDCスイープし，出力コードが切り替わる電圧点（遷移電圧）をすべて記録します．このデータが，静特性評価の最も基本的な生データとなります．
② 直線近似（線形成分の抽出）
得られた遷移電圧データを用いて，最小二乗法により直線近似を行います．
\(V = \alpha_0 + \alpha_1 \cdot \text{code}\)
ここで，
- \(\alpha_0\)：オフセット誤差（出力全体の上下シフト量）
- \(\alpha_1\)：ゲイン誤差（傾きのずれ，平均ステップ幅に相当）
この直線が，後のINL計算における「理想基準線」となります．
③ オフセット除去
直線当てはめで求めた \(\alpha_0\) を使って，
すべての遷移電圧からオフセット分を差し引きます．
\(V’ = V – \alpha_0\)
これにより，曲線全体が理想線の高さに揃い，純粋な傾きと形状のみが残ります．
④ 平均ステップ幅の算出
当てはめで得られた傾き \(\alpha_1\) が平均ステップ幅 \(\Delta_{\mathrm{avg}}\) に相当します．
\(\Delta_{\mathrm{avg}} = \alpha_1\)
これを基準にDNL／INLを計算することで，ゲイン誤差を除去した正しい非線形性を得ることができます．
⑤ DNL・INL算出
最後に，各コード幅および遷移点の偏差を計算します．
- DNL：各コード幅 \(\Delta_k\) のばらつき\(\mathrm{DNL}(k) = \frac{\Delta_k – \Delta_{\mathrm{avg}}}{\Delta_{\mathrm{avg}}}\)
- INL：各遷移電圧の理想直線からのずれ\(\mathrm{INL}(k) = \frac{V_k’ – V_{k,\mathrm{ideal}}}{\Delta_{\mathrm{avg}}}\)
コードが安定して切り替わる瞬間の電圧を正確に記録することが重要です．実際の評価でも，この流れを自動化した解析スクリプト（PythonやMATLABなど）がよく用いられます．この一連の処理を通して，ADCの非線形性を「線形成分を除去したうえで定量化」できるようになります．
補足:DAC(Digital to Analog Converter)のDNL/INLとの違い
今回の記事では，ADCにおけるDNL／INLを中心に解説してきましたが，同様の概念はDAC（Digital to Analog Converter：デジタル‐アナログ変換器）にも存在します．ただし，定義の取り方と評価の向きがADCとは少し異なります．
定義の基準点の違い
- ADC（A/D変換）入力電圧を基準として，遷移電圧 \(V_T\) が理想直線からどれだけずれるかを測定します．つまり，横軸（入力側）の非線形性を評価します．
- DAC（D/A変換）入力コードを基準として，出力電圧 \(V_\text{out}\) が理想直線からどれだけずれるかを測定します．こちらは，縦軸（出力側）の非線形性を評価する形になります．
INL(0) の扱いの違い
ADCでは，最初の遷移点 \(V_0\) が「入力の−∞から最初のコード境界」に対応するため，理想線上に比較点を持たず，INL(0) は定義されません．一方で，DACはすべてのコードに対応する出力電圧が実際に存在するため，INL(0) も含めてすべてのコードで定義可能です．
この違いは「どちらの軸を基準に線形性を測るか」という構造的な違いから生じています．
今回の記事では，ADCのINL/DNLについて扱いましたが，同様の定義がDAC(Digital to Analog converter)でもあります．図に示すと以下のようになります．
まとめ
本稿では，ADCのもうひとつの重要な性能指標である 非線形性（nonlinearity） と，それを数値で表す DNL／INL について学びました．これらは，これまで扱ってきた SQNR・ENOB などの「周波数領域の性能指標」とは異なり，静特性（入力と出力の直線性） を評価する指標です．
より優れたADCを作成するためには線形的な特性を持つことが重要です．そのために非線形性を定量的に理解し，その誤差を設計段階で補正することが欠かせません．
ポイントを振り返ると次のとおりです：
- 理想量子化器ではすべてのステップ幅（Δ）が等しく，入力と出力は直線関係を保つ．
- DNLとは「1ステップごとの“階段の均一さ”を測る指標．
→階段のステップが均一なほど優れている． - INLとは量子化特性全体の「曲がり具合」を示す指標．
→直線に近いほど優れている． - 線形誤差（ゲイン誤差・オフセット誤差） は非線形性とは別の要素であり，INL／DNLを求める前に補正して除去する必要がある．
以上です．最後まで読んでいただきありがとうございました．
これまで扱ってきた内容は，ADCの「システムレベル」の特性です．次回は視点を回路側に移し，なぜ非線形が生じるのか――スイッチ，アンプ，比較器などの回路非理想要素を掘り下げていきます．
参考文献
本記事はあくまで筆者の勉強備忘録のため，より正確に理解したい，さらに深く理解したい場合は下記をご参照ください．
- IIT Kanpur: https://www.iitk.ac.in
- SSCD Lab: https://iitk.ac.in/sscd
- 講義動画（YouTube）: https://youtu.be/cI7bYpW7EvE?si=uhuL8tSMJan23LHf
- 『アナログ/デジタル変換入門 ― 原理と回路実装 ―』 和保孝夫（監）／コロナ社
https://www.coronasha.co.jp/np/isbn/9784339009187 - 『ΔΣ型アナログ/デジタル変換器入門 第2版』 和保孝夫・安田彰（監訳）／丸善出版
https://www.maruzen-publishing.co.jp/book/b10120696.html
コメント