本記事は,アナログ・デジタル変換器(ADC)を題材に,筆者自身の理解を深める目的で整理している「ADC入門シリーズ」の一部です.シリーズ全体の方針や位置づけについては,以下の記事をご覧ください.
はじめに
前回の記事では,サンプリングスイッチを OFF にした瞬間に発生するチャージインジェクション が,S/H 回路の線形性を本質的に制限することを解説しました.
特に重要だったのは,問題は「電荷が注入されること」そのものではなく,その電荷が入力信号に非線形に依存することにある,という点でした.
本記事では,この問題に対する代表的な回路的解法であるボトムプレートサンプリング(bottom-plate sampling)について整理します.
チャージインジェクションの課題と対策の考え方
まず,前回記事の結論を簡単に振り返ります.
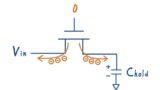
MOS スイッチが ON している間,チャネルには入力信号に依存したチャネル電荷 \(Q_{\text{ch}}(V_{\text{in}})\)が蓄積されています.このスイッチを OFF にすると,そのチャネル電荷の一部がホールド容量へ流れ込み,
\(\Delta V = \frac{\alpha Q_{\text{ch}}(V_{\text{in})}}{C}\)
という形で,入力依存の電圧誤差として現れます.ここで厄介なのは,
- \(Q_{\text{ch}}\) は入力信号の非線形関数
- \(\alpha\) は正確に制御できない
という点です.したがって,電荷を完全に無くすことはできないという前提に立ったうえで,その電荷をホールド容量に流れ込ませない構造を考える必要があります.
この思想を具体的な回路構造として実現したものが,ボトムプレートサンプリング になります.
ボトムプレートサンプリング
一般的な S/H 回路では,ホールド容量の片側(多くの場合は下側)が常に GND に接続されています.この構造では,サンプリングスイッチを OFF にした瞬間,MOS スイッチのチャネル電荷がホールド容量へ流れ込む明確な経路が存在します.
これは,スイッチ OFF = チャージインジェクションが直撃する という構造になっています.そこで発想を転換します.
スイッチを OFF にする瞬間,スイッチから見たインピーダンスが無限大に見えれば,電荷は流れ込めません.すなわち,「GND から切り離して OPEN にする」ことで,電荷の流入経路そのものを断つ,という考え方です.この考えを回路として実装したものが,ボトムプレートサンプリングです.
具体的には,サンプリング容量の下側(ボトムプレート)に,もう一つのスイッチ M2 を追加します.ここで最も重要なのは,スイッチの制御タイミングです.
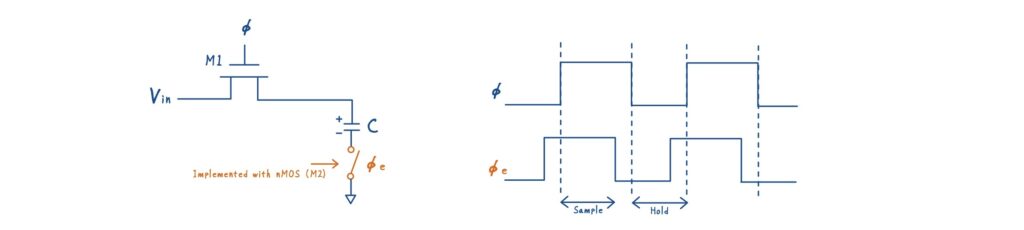
メインのサンプリングスイッチ M1 を制御するクロックを \(\phi\) とすると,ボトムプレート側のスイッチ M2 は,\(\phi\) より わずかに早く OFF される必要があります.
(M1 を OFF にする瞬間には,すでにボトムプレートは OPEN になっている,という状態を作ります)
この関係を満たすことで,M1 の OFF 遷移時に発生するチャネル電荷は,ホールド容量へ流れ込む経路を失います.これが,ボトムプレートサンプリングの基本原理です.
タイミングチャートを以下に整理します.
| \(\phi\) | \(\phi_e\) | |
| サンプリング状態 | ON | ON |
| メインスイッチOFFに備える準備状態 | ON | OFF |
| ホールド状態 | OFF | OFF |
実装上は,\(\phi_e\) を \(\phi\) の「早いバージョン」として生成する必要があるため,インバータチェーンなどを用いて意図的に遅延を与える構成が一般的です.
実装上の課題:オフ容量
ボトムプレートサンプリングでは,理想的には M2 を OFF にした瞬間,ボトムプレートは完全に OPENになっていてほしい,という前提があります.しかし実際の MOS スイッチでは,OFF にしてもドレイン–ソース間やゲート由来のオフ容量 \(C_{\text{off}}\) が必ず残ります.
その結果,回路は次のように見えてしまいます.
- メインのホールド容量 \(C\)
- ボトムプレート側に直列に接続された微小容量 \(C_{\text{off}}\)
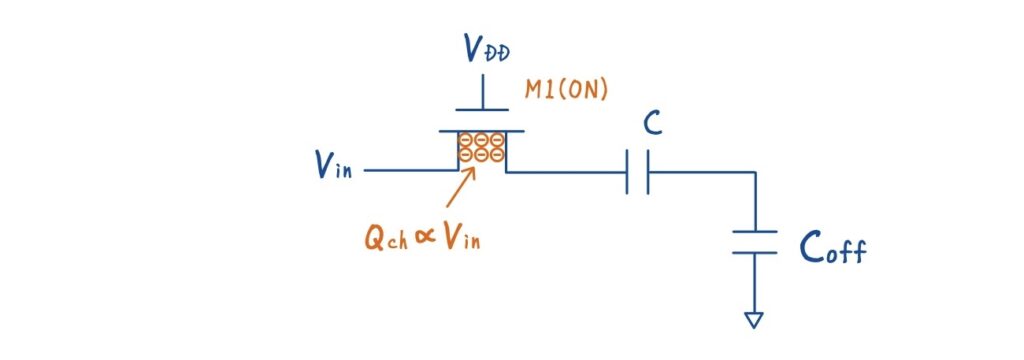
これは「完全な OPEN」ではなく,容量結合が残った状態です.
ここで,M1 が ON の間に蓄積されていたチャネル電荷を考えます.M1 のチャネル電荷は,\(Q_{\text{ch}} \propto V_{\text{in}}\)であり,入力信号に依存した量です.
M2 を OFF にすると,完全OPENならこの電荷は下側に流れ込めませんが,\(C_{\text{off}}\) が存在するため,チャネル電荷の一部 \(\beta Q_{\text{ch}}\) が容量結合を通じて下側へ結合してしまいます.
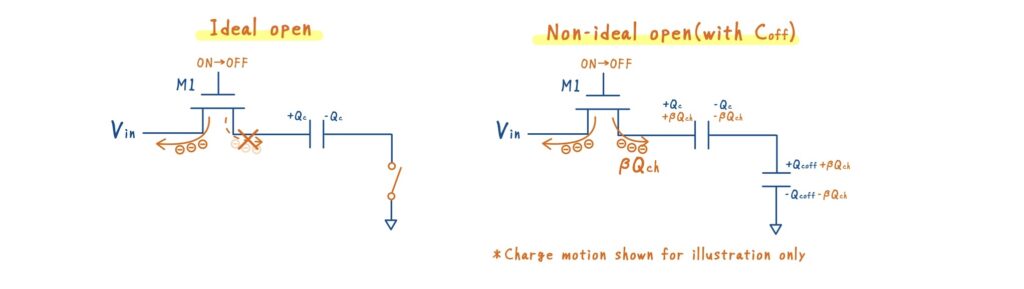
結局のところ,ボトムプレートサンプリングを行っても,\(C_\text{off}\) の存在によって,入力依存の非線形成分が再び現れるという問題が生じます.
しかし,ここで重要なのは,この現象は「電荷が注入された」こと自体が問題なのではなく,電荷の“見え方”をどう定義するかにあります.これは電荷の加減でうまくコントロールできます.
\(V_x\)と基準GND用スイッチ
前章で,オフ容量による容量結合によって,入力依存性を持った \(\beta Q_{\text{ch}}\) が注入される課題を指摘しました.ここで注目すべきなのが,ノード X に保存される全電荷 \(Q_x\) です.
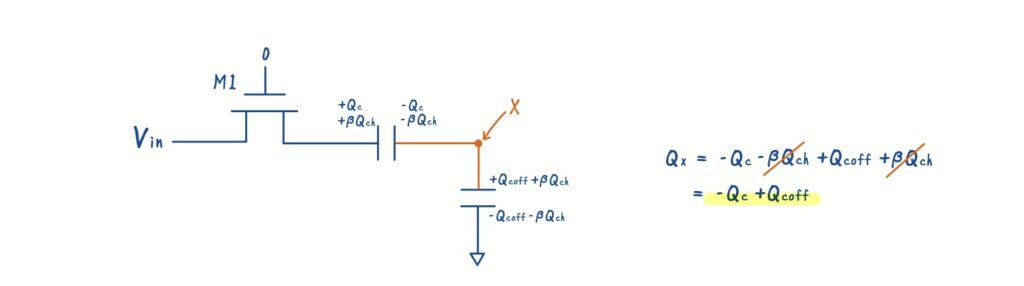
M1 を OFF にした瞬間,ノード X には以下の電荷がそれぞれ現れます.
- ホールド容量 \(C\) の − 側に \(-\beta Q_{\text{ch}}\)
- オフ容量 \(C_{\text{off}}\) の + 側に \(+\beta Q_{\text{ch}}\)
これらは同一ノード X に属する電荷であり,ノード X 全体として見たときの総電荷量 \(Q_x\) は変化していません.つまり,入力信号に非線形依存する \(\beta Q_{\text{ch}}\) は,ノード X の総電荷としては現れないという状態が作れています.この時点で,電荷のレベルではすでに「入力非線形性は除去されている」と言えます.
ただし,ここで一つ重大な問題があります.ノード X は DC 的にどこにも接続されておらず,浮遊ノードです.浮遊ノードでは,絶対電位が定義できず,寄生容量や過去の履歴に依存して電圧が決まるなどの問題があり,そのままでは「電圧」として扱えません.そこで,サンプリングが完了した後に,下図に示すように,一度 GND へ接続するという作業を行います.
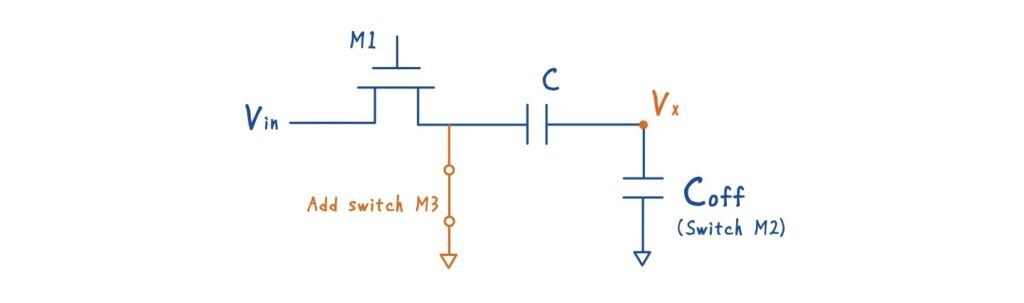
このとき,ノード X の電荷と電圧は次のようになります.
\(Q_x = Q_{\text{off}} – Q_C\)
\(V_x = \frac{Q_x}{C + C_{\text{off}}} \approx -\frac{C}{C + C_{\text{off}}} V_{\text{in}}\)
\(C_{\text{off}} \ll C\) が成り立つ領域では,\(V_x \approx -V_{\text{in}}\)と近似できます.この作業によって,入力に非線形依存する誤差成分を含まない,本来サンプリングしたかった \(V_{\text{in}}\) に比例する電圧を得ることができます.
もちろん,この GND 接続も常時行うことはできません.そのため,下図のように基準電位を作るためのスイッチ M3が追加され,これもクロック制御されることになります.この制御シーケンスについては,次の章で詳しく整理します.
制御シーケンス
ボトムプレートサンプリングでは,回路構成だけでなく,スイッチをどの順番で ON/OFF するかが極めて重要になります.適切なシーケンスが守られなければ,これまで議論してきた電荷の差分構造や非線形性の抑制は,一瞬で崩れてしまいます.

基本となる動作は,次の 2 つのフェーズです.
サンプル(Sample)
- メインスイッチ M1:ON
- ボトムプレートスイッチ M2:ON
- GND スイッチ M3:OFF
この期間,ホールド容量には入力信号 \(V_{\text{in}}\) が追従し,\(Q = C \cdot V_{\text{in}}\) の電荷が蓄えられます.この時点ではチャネル電荷も存在しますが,まだ問題は顕在化していません.
ホールド(Hold)
ホールド状態へ移行する際には,必ず次の順番を守ります.
1.ボトムプレートスイッチ M2 を先に OFF
2.メインスイッチ M1 を OFF
3.最後に GND スイッチを ON
この順序により,M1 の OFF に伴うチャネル電荷は,ノード X では差分として相殺され,電圧誤差として現れません.すなわち,チャネル電荷そのものは発生していますが,入力に非線形依存する成分は電圧として観測されない状態が実現されます.
非重畳クロックが必要な理由
この動作を成立させるためには,各スイッチを制御するクロックが非重畳でなければなりません.
もし,
- M1 と GND スイッチが同時に ON
- M2 が ON のまま M1 を OFF
といった瞬間が存在すると,チャージインジェクションが再びホールド容量へ直撃し,これまで構築してきた差分構造は破壊されます.
そのため実装では,1 つのマスタークロック \(\phi_{\text{CLK}}\) から,遅延回路や論理回路を用いて,\(\phi\),\(\phi_e\),\(\phi_x\)といった非重畳クロックを生成します.非重畳性は回路側で保証する,というのが実務的な設計方針です.
シーケンス設計の本質として強調しておきたいのは,ボトムプレートサンプリングの目的は,”電荷を消すこと”,”チャネル電荷を無くすこと”ではない,という点です.本質は,問題となる電荷が,問題となるノードに電圧誤差として現れる瞬間を作らないことにあります.そのために,回路構造と制御シーケンスを同時に設計しているのが,ボトムプレートサンプリングです.
まとめ
本稿では,チャージインジェクションの課題に対して,その代表的な回路的解法である ボトムプレートサンプリング について解説しました.重要なのは,入力依存性を持つ電荷がどのノードに,どのタイミングで,どのように現れるかという観点で整理することでした.
ポイントを振り返ると,次のとおりです:
- S/H 回路において,スイッチ OFF への切り替え時にチャネル電荷が,ホールド容量へ直接流れ込む経路を持つ.
- ボトムプレートサンプリングでは,サンプリング容量の下側を一度 OPEN にすることで,この電荷流入経路を断つ.
- 実際にはオフ容量 \(C_{\text{off}}\) が存在するが,結合した電荷はノード X 上で差分として現れ,入力非線形性は電圧誤差として観測されない.
- ノード X は浮遊ノードであるため,電圧として扱うには基準電位(GND)を与える操作が必要となる.
- ボトムプレートサンプリングでは,回路構造と制御シーケンス(非重畳クロック)を一体で設計することが不可欠である.
以上のように,ボトムプレートサンプリングは,「非線形な電荷を無くす」のではなく,非線形な電荷が電圧誤差として現れないように回路と時間を設計する手法です.
次回は,ここで登場した「基準電位を与える」という考え方をさらに発展させ,オペアンプを用いた仮想 GND による実装について解説します.
以上です.最後まで読んでいただきありがとうございました.
参考文献
本記事はあくまで筆者の勉強備忘録のため,より正確に理解したい,さらに深く理解したい場合は下記をご参照ください.
- IIT Kanpur: https://www.iitk.ac.in
- SSCD Lab: https://iitk.ac.in/sscd
- 講義動画(YouTube): https://youtu.be/cI7bYpW7EvE?si=uhuL8tSMJan23LHf
- 『アナログ/デジタル変換入門 ― 原理と回路実装 ―』 和保孝夫(監)/コロナ社
- 『ΔΣ型アナログ/デジタル変換器入門 第2版』 和保孝夫・安田彰(監訳)/丸善出版

(ADCの基礎を一通り確認する目的で,最初の一冊として取り組みやすい内容です.価格も,専門書の中では比較的手に取りやすいと思います.)

(筆者が所持しているのは第 1 版ですが,こちらも分かりやすくておすすめです.)