ADC入門 -S/H回路の熱雑音（Thermal Noise）- nanaloglab

はじめに
抵抗に生じる熱雑音
RC 回路における熱雑音
S/H 回路の熱雑音
サンプリング後の熱雑音 PSD とその性質
S/H 回路の容量値設計
まとめ
参考文献

はじめに

前回までの記事では，S/H（Sample & Hold）回路の構成とスイッチの非線形性について学びました．オン抵抗の非線形性の要因と，改善策としてゲート・ブートストラップ回路を解説しています．

ADC入門 -ゲート・ブートストラップ・スイッチ(Gate Bootstrap Switch)-

ブートストラップスイッチの目的とその役割についてわかりやすく解説します．回路実装をトランジスタ一つずつ丁寧にまとめました．

本稿では，S/H 回路の性能限界を決める要素のひとつである熱雑音について整理します．
これまでに見てきたスイッチのオン抵抗に加えて，トランジスタの寄生成分や容量に由来するものなど，アナログ回路設計において見逃せない非理想性は至る所に存在します．その中でも最も根源的で，しかも避けることのできないのが，本記事で扱う熱雑音（thermal noise）です．

特に S/H 回路で支配的となるのが，\(\frac{kT}{C}\) で表される雑音パワーであり，これはどれほど優れたスイッチを用いても絶対にゼロにはできない物理的限界です．本稿では，この熱雑音が ADC の性能にどのように影響を及ぼすのかを，図と式を用いて丁寧に解説していきます．

抵抗に生じる熱雑音

抵抗に熱雑音が生じる理由は，抵抗内部の電子が温度が \(0\,\mathrm{K}\) より高い限り熱エネルギーを受けてランダムに運動していることに起因します．電子がランダムに運動することで，抵抗の両端には電流が流れていなくても電圧のゆらぎが誘起されます．これが熱雑音です．この現象は「ジョンソンノイズ（Johnson–Nyquist noise）」とも呼ばれ，抵抗に必ず存在する熱ゆらぎとして知られています．（詳細は ▶ ジョンソンノイズで検索するとより深い解説が得られます．）

解析を扱いやすくするため，ノイズ計算では等価モデルがよく用いられます．抵抗そのものは「ノイズを持たない理想抵抗」とし，ノイズ（雑音）は仮想的な電圧源 \(v_\mathrm{n}\) または電流源 \(i_\mathrm{n}\) に集約して表現します．これによって，回路中でのノイズ伝搬を解析しやすくなります．

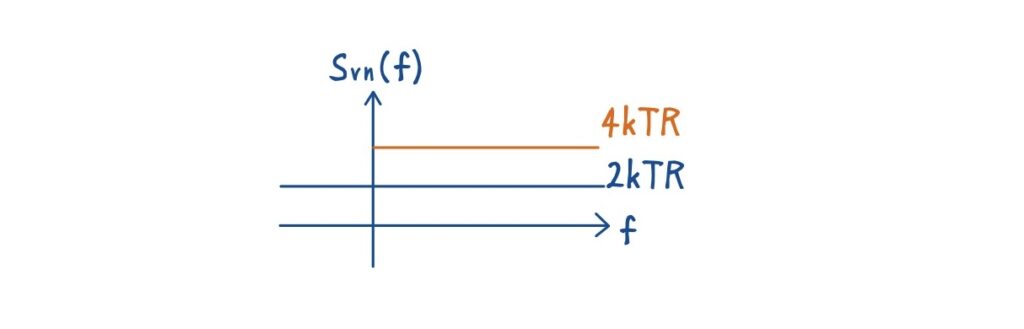
ノイズ解析で重要なのは，熱雑音がランダムであるため，統計量として扱うという点です．平均値は 0 であり，周波数領域でのゆらぎはパワースペクトル密度（PSD）で表されます．アナログ回路で一般的に使用される片側 PSD では，熱雑音の PSD は次式で与えられます．

\(S_{v_\text{n}}(f)=4kTR \quad [\mathrm{V^2/Hz}]\)

\(k = 1.38\times10^{-23}\,\mathrm{J/K}\)（ボルツマン定数）
\(T\)：絶対温度
\(R\)：抵抗値

例えば \(T=300\,\mathrm{K}，R=50\,\Omega\) の抵抗であれば，

\(S_{v_\text{n}} \approx 8.28\times10^{-19}\,\mathrm{V^2/Hz}\)

の熱雑音が存在します．

熱雑音は一般に白色雑音（ホワイトノイズ）とみなされ，PSD はすべての周波数で一定と考えられます．厳密には全帯域で完全に平坦ではありませんが，THz オーダーまではほぼ一定であり，実際のアナログ回路が扱う周波数帯域では十分に平坦とみなせます．

補足として，熱雑音の PSD には両側 PSD（two-sided PSD）と片側 PSD（one-sided PSD）の 2 種類の定義があります．理論的には両側 PSD の

\(S_{v_\text{n}}(f)=2kTR \quad (f\in -\infty\sim +\infty)\)

が自然ですが，実際のアナログ回路設計や測定では負の周波数は存在しないため，0〜∞ の周波数帯で扱う片側 PSD（4kTR）が仕様として採用されます．これは，総雑音パワーの面積を一致させるため，片側 PSD を 2 倍にしているだけです．

RC 回路における熱雑音

続いて，RC 回路における熱雑音について考えます．以前の記事で述べたように，S/H 回路はスイッチが ON の間，スイッチのオン抵抗 \(R_\text{on}\) とホールド容量 \(C\) から構成される RC 回路と見なすことができます．したがって，RC 回路に流れ込む熱雑音のふるまいを理解することは非常に重要です．

ここでは，先ほど定義した理想抵抗＋雑音源（電圧源モデル）と容量で構成される RC ローパスフィルタを想定し，その出力に現れるノイズを解析します．入力 PSD は抵抗の熱雑音なので片側 PSD で \(4kTR\) です．このノイズが RC の伝達関数によって減衰し，出力に現れます．RC フィルタの伝達関数は次式です．

\(H(f)=\frac{1}{1+j\,2\pi fRC}\)

したがって，出力側のパワースペクトル密度（PSD）は次式です．

\(S_{v_{\text{out}}}(f) =4kTR\cdot\left|H(f)\right|^2 =4kTR\cdot\frac{1}{1+\left(2\pi fRC\right)^2}\)

出力ノイズの総パワーは，この出力 PSD を \(f=0\) から \(\infty\) まで積分することで求まります．途中式も含めて示すと，次のようになります．

\(\int_{0}^{\infty} S_{v_{\text{out}}}(f)\,df =\int_{0}^{\infty} 4kTR\cdot\frac{1}{1+\left(2\pi fRC\right)^2}\,df =\frac{kT}{C}\)

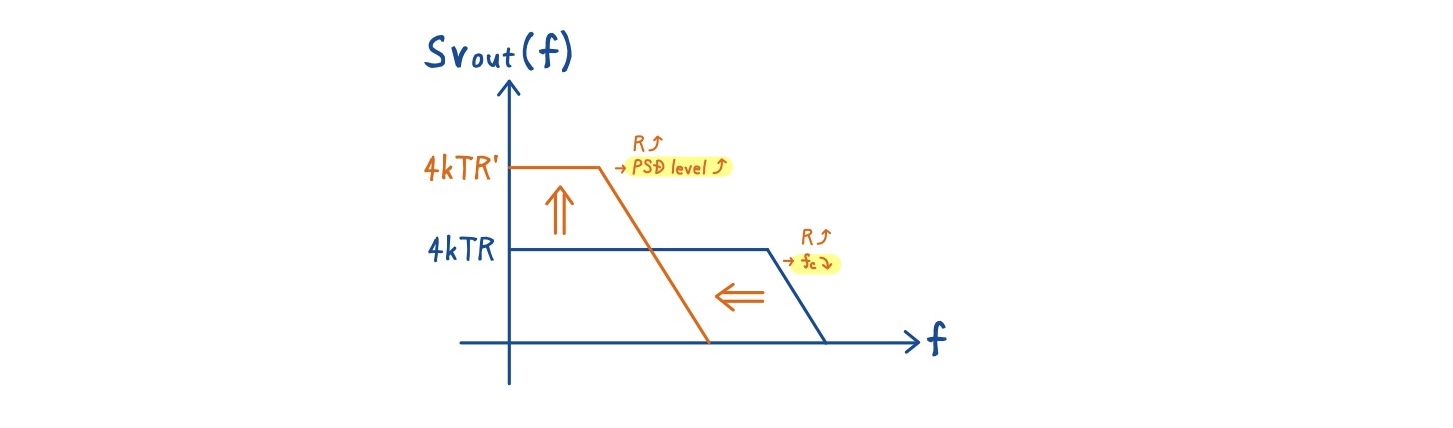
ここで特に重要なのは，熱雑音源は抵抗であるにもかかわらず，最終的な出力ノイズパワーは抵抗値 R に依存しないことです．一見すると直感に反するように思えますが，下図のように考えると理解しやすくなります．

低周波領域のノイズ PSD のレベル（高さ）はRに比例
カットオフ周波数 \(1/(2\pi RC)\) は低くなり，通過帯域（横方向）は R に反比例

この 2 つの効果がちょうど打ち消し合うため，PSD の積分面積（＝雑音パワー）は常に一定になります．その結果，出力雑音パワーは \(\frac{kT}{C}\) に必ず落ち着き，抵抗値によらない普遍的な値となります．

RC回路熱ノイズの積分の計算過程

出力 PSD と出力雑音パワーは次式で示しました．ここから，\(kT/C\)までの導出過程が少し複雑なので残しておきます．

\(S_{v_{\text{out}}}(f) = 4kTR \cdot \frac{1}{1 + (2\pi fRC)^2}\)

\(\int_0^{\infty} 4kTR \cdot \frac{1}{1 + (2\pi fRC)^2}\,df\)

変数変換を行い，\(x = 2\pi fRC\) とおくと，下式が得られます．

\(df = \frac{1}{2\pi RC}\,dx\)

これを代入すると，次のように書き換えられます．

\(\int_0^{\infty} 4kTR \cdot \frac{1}{1 + x^2} \cdot \frac{1}{2\pi RC}\,dx\)

定数項を外に出すと，

\(\frac{4kTR}{2\pi RC} \int_0^{\infty} \frac{1}{1 + x^2}\,dx\)

ここで現れる積分は，よく知られた形です．

\(\int \frac{1}{1 + x^2}\,dx = \tan^{-1}(x)\)

したがって，

\(\int_0^{\infty} \frac{1}{1 + x^2}\,dx = \left[ \tan^{-1}(x) \right]_0^{\infty} = \frac{\pi}{2}\)

これを元の式に戻すと，

\(\frac{4kTR}{2\pi RC} \cdot \frac{\pi}{2} = \frac{kT}{C}\)

となり，最終的な結果が得られます．

\(\int_0^{\infty} S_{v_{\text{out}}}(f)\,df = \frac{kT}{C}\)

S/H 回路の熱雑音

S/H 回路の熱雑音について考えます．前章の RC フィルタにおける熱雑音の結果を，そのまま S/H 回路に応用することができます．（ここではホールド容量を \(C_{\text{hold}}\) と表記しますが，前節の容量 C と同じ物理量です．）

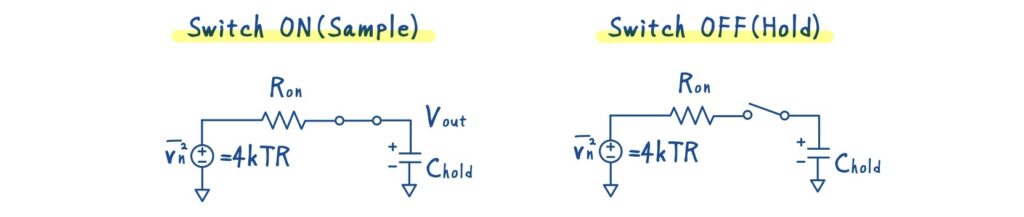
S/H 回路では，動作をスイッチ ON（サンプル時）とスイッチ OFF（ホールド時）の二つに分けて考える必要があります．

スイッチ ON（サンプル時）

スイッチが ON になると，スイッチのオン抵抗 \(R_{\text{on}}\) を通じて抵抗の熱雑音（\(4kTR_{\text{on}}\)）がホールド容量 \(C_{\text{hold}}\) に注入されます．

このとき，\(C_{\text{hold}}\) には前のクロック周期でサンプルされた雑音（初期条件）が残っている場合があります．そのため，サンプル期間中には次の二つの作用が同時に働きます．

1．前サイクルで \(C_{\text{hold}}\) に残っている雑音（初期条件）
2．今回のサイクルで新たに注入される雑音

しかし，\(R_{\text{on}}\) と \(C_{\text{hold}}\) がつくる RC 時定数が十分に小さければ，これらは次のサイクルへ影響を持ち越しません．

スイッチオン時間を \(T_{\text{on}} \approx T_s/2\) とすると，

\(R_{\text{on}}\,C_{\text{hold}} \ll T_s/2\)

を満たす場合，初期条件はスイッチ ON の間に指数的に減衰し，ほぼ 0 になります．

結果として，連続する出力サンプル間には相関がなくなり，離散時間ノイズは統計的に独立になります．この性質こそが，離散時間 PSD が白色（ホワイトノイズ）になる理由です．サンプル間の相関が十分に小さくなる（ほぼ独立になる）とき，自己相関関数は δ 関数状となり，PSD はフラットになります．このサンプル間相関を決定づけているのが，S/H 回路の時定数 \(R_{\text{on}}C_{\text{hold}}\) です．

スイッチ OFF（ホールド時）

スイッチが OFF になると，雑音源であるオン抵抗 \(R_{\text{on}}\) は回路から完全に切り離されます．

したがって，\(C_{\text{hold}}\) は外部から雑音が流れ込まず，\(C_{\text{hold}}\) の電荷は理想的には変化しない（＝サンプル値を保持するだけ）という状態になります．

つまり，S/H 回路の熱雑音はスイッチ ON の瞬間だけで決まり，ホールド中に雑音が追加されることはありません．ホールド期間はあくまでサンプル値を保持するだけのフェーズであり，ノイズ解析上は「静的」として扱えます．

サンプリング後の熱雑音 PSD とその性質

サンプリング周波数 \(f_s\) で標本化すると，スペクトルは周波数領域で \(f_s\) 間隔で周期的に複製され，折り返し（aliasing）として基帯域（\(0〜f_s/2\)）へ重なります．この性質は熱雑音でも同様で，連続時間のノイズ PSD がそのまま周期複製されて重ね合わさるだけです．

連続時間 RC 回路の出力ノイズの総面積（分散）は常に次式で与えられます．

\(\int_0^{\infty} S_{v_{\mathrm{out}}}(f)\,df = \frac{kT}{C_{\text{hold}}}\)

サンプリングによってスペクトルを複製しても，折り返しによって基帯域へ戻ってくるだけで，総面積（分散）は一切変化しません．したがって，離散時間で得られるノイズサンプル列の分散も次式になります．

\(\mathrm{Var}[v[n]] = \frac{kT}{C_{\text{hold}}}\)

ここで注意すべき点は，総パワー（面積）は一定でも，PSD の“高さ”はサンプリング周波数に依存して変化するということです．連続時間の抵抗が発生するノイズ PSD（4kTR）よりも高いレベルに見える場合があるのは，折り返し成分が基帯域で重なるためであり，ノイズが増加したわけではありません．

離散時間の PSD は次式のように，元の PSD を \(f_s\) ごとに複製して足し合わせたものになります．

\(S_{dd}(f) \propto \sum_{k=-\infty}^{\infty} S_{\text{analog}}(f-kf_s)\)

この式から直感的に分かるように，

\(f_s\) が大きいほど複製の間隔が広がり，折り返しが減るため PSD は低く見える．
\(f_s\) が小さいほど複製同士が近づき，折り返しが密集するため PSD は高く見える．

つまり，サンプリング周波数が低いと狭い帯域に多くの複製が重なるため「密度」が上がり，逆に \(f_s\) が高いと広い帯域に分散されるため「密度」が下がるという理解ができます．\(f_s\) を 2 倍にした場合，分散は一定のまま観測帯域が 2 倍に広がるので，PSD の高さは半分（−3 dB）になります．

サンプリング周波数が低いほど「粗く読む」ことになるため，小さな誤差が目立ちやすいという感覚にも一致します．このように，サンプリングによって PSD の形状や高さは変化しても，総ノイズパワー（kT/C）は常に一定であるという点を理解しておくことが，ADC のノイズ解析において非常に重要です．

S/H 回路の容量値設計

これまでの議論から分かるように，S/H 回路の熱雑音はホールド容量 \(C_{hold}\) によって決まります．ノイズの二乗平均値は常に kT/C に収束するため，容量値は ADC の性能限界を直接支配します．

ホールド容量値の選択には明確なトレードオフがあります．容量を小さくすると回路面積が減り，スイッチが駆動すべき電荷量も減るため消費電力が小さくなります．一方で，容量を大きくすると熱雑音が減少し，容量の製造ばらつき（ミスマッチ）も相対的に小さくなります．この両者のバランスを見極めることが設計上の大きなポイントです．表にまとめると次のようになります．

	容量を小さくする（C↓）	容量を大きくする（C↑）
熱雑音 kT/C	× 大	◎ 小
ミスマッチ（ばらつき）	× 大	◎ 小
回路面積	◎ 小	× 大
消費電力	◎ 小	× 大
サンプリング速度	◎ 高速動作	× 速度低下

熱雑音から必要容量の見積もり

例として，13 bit の分解能を持つ ADC を設計する場合を考えます．仮に 1 LSB の 1/10 程度までのノイズ誤差を許容するという前提条件のもとで，LSB を \(\mathrm{LSB} = \frac{V_{\mathrm{FS}}}{2^{13}}\) とすると，ノイズ条件は下式になります．

\(\sqrt{\frac{kT}{C_{hold}}} = \frac{\mathrm{LSB}}{10}\)

両辺を二乗して整理すると，必要なホールド容量 \(C_{hold}\) は，

\(C_{hold} = 100 \cdot \frac{kT}{\mathrm{LSB}^2}\)

フルスケール \(V_{\mathrm{FS}} = 1\,\mathrm{V}\)，温度 \(T = 300\,\mathrm{K}\) とすれば，容量は数十 pF 程度になります．

このようにして，熱雑音から S/H 回路に必要な最小容量を手計算で見積もることができます．
ただし，実際には容量の製造ばらつき（ミスマッチ）から計算される容量値がこれよりも大きいこともあり，その場合は，ばらつきの方が支配的になるため，ファウンドリの PDK が示す最小容量が容量設計の下限になることもよくあります．

オーバーサンプリング（OSR）

オーバーサンプリング（OSR）を用いると，入力帯域におけるノイズパワーは OSR 倍に分散されるため，帯域内のノイズ電力は \(1/\mathrm{OSR}\)，ノイズの RMS 値は\(1/\sqrt{\mathrm{OSR}}\) まで低減されます．したがって，同じノイズレベルを維持するために必要なホールド容量は

\(C_{\mathrm{OSR}} = \frac{1}{\mathrm{OSR}}\,C_{\mathrm{original}}\)

例えば OSR = 2 の場合，必要な容量は元の 1/2 まで削減できます．

まとめ

本稿では，S/H（Sample & Hold）回路における熱雑音を出発点として，回路レベルでの振る舞い，さらに容量設計への落とし込みまでを順を追って整理しました．

S/H 回路のノイズ特性は ADC の分解能や SNR を直接支配するため，そのメカニズムを正しく理解しておくことは非常に重要です．

ポイントを振り返ると次のとおりです：

抵抗には，電子の熱運動に起因する熱雑音が必ず存在する．　
→ 片側 PSD では 4kTR で表される白色雑音としてモデル化できる．
RC ローパスフィルタの出力ノイズの総パワーは常に \(\frac{kT}{C}\) になる．
S/H 回路では，ノイズが注入されるのはスイッチ ON（サンプル時）だけである．　
→ スイッチ OFF（ホールド時）にはノイズ源が切り離され，新たなノイズは加わらない．
\(R_{\text{on}}C_{\text{hold}} \ll T_s/2\) を満たすと，サンプル間の相関が消え，離散時間ノイズは白色 PSD を持つ．
S/H 回路のPSD の「高さ」はサンプリング周波数 \(f_s\) に依存する．　
→ ただし，総ノイズパワー（分散）は常に \(\frac{kT}{C}\) となる．
S/H 回路の熱雑音は容量を大きくするとノイズは減る．
→ただし面積・消費電力は増え，明確なトレードオフがある．
OSRを用いると，信号帯域内のノイズ密度は\(1/\sqrt{\mathrm{OSR}}\) に低減できる．