本記事は,アナログ・デジタル変換器(ADC)を題材に,筆者自身の理解を深める目的で整理している「ADC入門シリーズ」の一部です.シリーズ全体の方針や位置づけについては,以下の記事をご覧ください.
はじめに
前回までの記事では,スイッチトキャパシタ(Switched Capacitor,以下 SC)回路の基本動作を整理し,その回路解析を実施しました.回路解析では,ラプラス変換を用いたKCLの解法についても触れました.
連続時間の動的システムを解析するためには,ラプラス変換を用いるのが便利です.同じように,離散時間のシステムを解析するためには 本記事で触れるZ変換が用いられます.
スイッチトキャパシタ(SC)回路のように,クロックによって状態が更新される系は,本質的に離散時間で記述するのが自然です.本稿では,Z変換の定義を押さえたうえで,Z変換を用いた伝達関数表現 (H(z))(差分方程式 → (H(z)))までを扱います.
正直,Z変換については,本記事でまとめずとも有益な記事や説明文書は多々あります.詳細に理解したいかたはそちらをご参照ください.本記事では,アナログ回路設計者がシステムを理解する・設計する上での視点ベースでまとめています.
参考文献:やる夫で学ぶディジタル信号処理 z変換
(やる夫で学ぶシリーズにはいつもお世話になっています.)
z変換の意義
ここでは,回路設計者の目線で,Z変換を学ぶ意義について考えます.
これまでに学んだスイッチトキャパシタ(SC)回路は,ADC設計において最重要クラスの回路ブロックのひとつです.SC回路の信号はクロック境界で状態が更新されるため,本質的には離散時間の変化です.このとき頻出するのが,「前のサイクルでサンプルした値が,次のサイクルで効く」という 1クロック遅延です.
Z変換を使うと,この遅延を \(z^{-1}\) という形で表現できます.
Z変換の大きなメリットは,回路動作を差分方程式として整理し,そのまま伝達関数の導出に落とし込めることです.結果として,回路の振る舞いを代数計算として扱えるようになります.これは,連続時間の回路解析でラプラス変換を用いることで,微分方程式を直接解かずとも代数計算に持ち込めることに似ていますね.
さらに,伝達関数 \(H(z)\) が得られると,離散時間系の周波数特性(利得や位相)も同じ枠組みで整理できるようになります.時間領域の式だけでは見えにくい「どの周波数帯を通し,どの周波数帯を抑えるか」といった性質を,設計者の観点で見通しよく扱える点も大きなメリットです.また,フィードバック系では回路の安定性が極めて重要です.Z変換を用いると,安定性を決める要因(極の位置など)を z 平面上で整理でき,設計者としての理解や見通しが得やすくなります.
例えば,今後登場するSC積分器は,「クロックごとに状態が積み上がる」回路です.その解析と設計へ進む準備として,本記事ではまず z 領域の作法を揃えます.
z変換の定義
回路設計に関する文脈でまず使うのは 片側Z変換です.実際の回路を解析するときには,ある時刻から動作が開始し,初期条件(初期状態)が与えられる状況を扱うことが多いためです.その意味で,時刻0以降を自然に記述できる片側Z変換は,回路解析と相性が良い形式になっています.
片側Z変換は,次で定義されます.
\(X(z)=\sum_{n=0}^{\infty}x[n]z^{-n}\)
本稿では数学的な導出や厳密な定義には踏み込まないので,定義の丸暗記ではなく,まずは \(z^{-n}\) が示す意味を押さえます.
\(z^{-n}\) は「nサンプル前(nクロック前)の寄与」を表しており,Z変換は「過去の影響を (z^{-1}) で整理しながら足し合わせたもの」と捉えると扱いやすくなります.
- (\z^{-1}\):1サンプル遅れ(1クロック遅れ)
- (\z^{-2}\):2サンプル遅れ(2クロック遅れ)
補足:片側Z変換と両側Z変換
片側Z変換は \(n\ge 0\) を対象とし,時刻0以降の信号を扱います.回路解析では,初期条件を含めて「ある時刻から動作を開始する」状況を記述できるため,片側Z変換が自然です.
両側Z変換は \(n\) を \(-\infty\) から \(+\infty\) まで扱う一般形で,理論的に便利です.
本稿ではSC回路(時刻0以降の動作と初期条件を前提とする解析)を扱うため,以降は片側Z変換を前提にします.
定義に従って,簡単な例を計算してみます.
\(x[0]=2,\;x[1]=3,\;x[2]=-4,\;x[3]=5,\;x[4]=2\)
のような離散時間信号に対し,Z変換は
\(\begin{aligned}
X(z)
&=\sum_{n=0}^{\infty}x[n]z^{-n} \
&=2+3z^{-1}-4z^{-2}+5z^{-3}+2z^{-4}
\end{aligned}\)
となります.(ここでは \(n\ge 5\) で \(x[n]=0\) とみなしています.)
この例から分かるように,離散時間で「1つ前の値」を使う操作は,z 領域では \(z^{-1}\) を掛けるだけです.この性質を理解すると,Z変換がイメージしやすくなり,使える形になってきます.
\(\mathcal{Z}{x[n-1]}=z^{-1}X(z)\)
SC回路で言えば,「\(\phi_1\)でサンプルした値が,次の\(\phi_2\)で出力に反映される」という動作が,この形で記述できます.
z領域における伝達関数の導出
回路を z 領域で扱う際の基本手順は,時間領域で差分方程式を立て,それをZ変換して 伝達関数 H(z) に変換することです.例として,簡単な一次系を示します.
\(y[n]=a\,y[n-1]+b\,x[n]\)
定義に従って,Z変換すると,下記になります.
\(Y(z)=a\,z^{-1}Y(z)+bX(z)\)
したがって,伝達関数H(z)は下式で示すことができます.
\(H(z)=\frac{Y(z)}{X(z)}=\frac{b}{1-a z^{-1}}\)
ここまで到達できれば,「離散時間の回路」を z 領域のフィードバック系として見通せます.
次の章では,この流れをSC回路の具体例で確認します.
SC アンプのZ変換
これまでの記事で扱った典型的な2相SCアンプについて,z領域での伝達関数を求めていきます.下図の回路を想定し,入力サンプル用の容量を \(C_{S}\),帰還容量を \(C_{F}\) とします.オペアンプは理想(ゲイン無限,仮想接地,入力電流0)と仮定します.
本稿では,サイクル境界を基準に次のように定義します.
- \(x[n]\):n回目の \(\phi_1\) でサンプルされた入力
- \(y[n]\):n回目の \(\phi_2\) 終了時点で確定した出力
入力は \(\phi_1\) で取り込まれ,出力は \(\phi_2\) で確定するため,n回目の出力 \(y[n]\) は 1つ前にサンプルされた \(x[n-1]\) によって決まります.
またこの例題では,積分器にしないために \(\phi_1\) で \(C_{F}\) をリセットし,サイクル開始時の出力を基準状態の0に戻すものとします.
差分方程式から伝達関数の導出
(n−1)回目の φ1 で,\(C_{S}\) は入力 \(x[n-1]\) をサンプルし,次の電荷を保持します.
\(Q_{S}=C_{S}\,x[n-1]\)
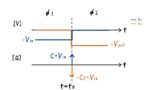
(n−1)回目の φ2 で \(C_{S}\) をノードXへ接続すると,ノードXは仮想接地(ほぼ0V)に保たれます.結果として \(C_{S}\) の両端電圧は\(0V\)へ移行し,\(C_{S}\) が保持していた電荷の変化分が \(C_{F}\) へ転送されます.
電荷保存より,\(\Delta Q_{F}=-Q_{S}=-C_{S}\,x[n-1]\)
一方で,n回目の \(\phi_1\) では \(C_{F}\) をリセットしているため,n回目の \(\phi_2\) では \(C_{F}\) の電荷は0からスタートします.またノードXは0Vなので,\(\phi_2\) 終了時点の \(C_{F}\) の電荷は出力 \(y[n]\) で
\(\Delta Q_{F}=C_{F}\,y[n]\)
と書けます.したがって,
\(C_{F}\,y[n]=-C_{S}\,x[n-1] \Rightarrow y[n]=-\frac{C_{S}}{C_{F}}\,x[n-1]\)
となります.ここで,\(k\equiv \frac{C_{S}}{C_{F}}\)と置けば,
\(y[n]=-k\,x[n-1]\)
前章で学んだ遅延の性質(\(\mathcal{Z}\{x[n-1]\}=z^{-1}X(z)\))を用いれば,下式がもとまります.
\(Y(z)=-k\,z^{-1}X(z) \Rightarrow H(z)=\frac{Y(z)}{X(z)}=-k\,z^{-1}\)
この結果が示すポイントは下記の2つです.
- ゲインは容量比 \(k=C_{S}/C_{F}\) で決まる.
→こちらは前回,前々回記事の結論と同じです. - \(z^{-1}\) は「サンプルしてから出力が確定するまで1クロック遅れる」ことを表す.
極,零点,安定性
伝達関数\(H(z)\) が得られたら,次に注目するのは分母と分子です.Z変換をやる意義,これによって,システムの安定性がどうかを理解しやすくなります.
ここで,重要になる極と零点は下記を意味します.
- 分母が0になる点:極(pole)
- 分子が0になる点:零点(zero)
例えば,一次系 \(H(z)=\frac{b}{1-a z^{-1}}\) では,分母 \(1-a z^{-1}=0\) から極は \(z=a\) と読めます.極は応答の支配要素であり,\(|a|\) が1に近いほど「過去の影響が長く残る」=応答が遅くなります.逆に \(|a|\) が小さいほど,過去の影響は速く減衰し,応答は速く収束します.
因果な離散時間系の安定性は,極の位置で判断できます.
- すべての極が単位円内((|p|<1))なら安定
- 単位円上または外側に極があれば不安定
ここで単位円とは,z平面上の \(|z|=1\) の円です.
[図5:z平面,単位円,極が内側と外側の比較]
このあたりの説明も下記サイトが詳細で分かりやすいです.
ラプラス変換との対応:(z=e^{sT})
最後に,ラプラス変換との対応もまとめておきます.冒頭で述べたように,連続時間の回路解析ではラプラス変換を用いることで,微分方程式を代数的に扱えるようになります.同様に,離散時間の解析でもZ変換を用いることで,差分方程式を代数的に扱えるようになります.
ここで,ラプラス変換の定義を復習しておきます.
\(\mathcal{L}\{x(t)\}=X(s)=\int_{0}^{\infty} x(t)\,e^{-st}\,dt\)
ラプラス変換では,連続時間の指数モード \(e^{st}\) を基本要素として扱います.一方,離散時間では \(t=nT\)(\(T\) はサンプリング周期)で値を観測するため,
\(e^{st}=e^{s nT}\)
となります.ここで \(z=e^{sT}\)と置けば,
\(e^{s nT}=(e^{sT})^{n}=z^{n}\)
と書けます.つまり,連続時間の指数モード \(e^{st}\) は,離散時間では \(z^{n}\) に対応します.
この対応により,ラプラス領域で「左半平面で安定(\(\mathrm{Re}(s)<0\))」という感覚を,離散時間の「単位円内で安定(\(|z|<1\))」へ置き換えることができます.さらに,s 平面上の極 \(s=p\) は \(z=e^{pT}\) に写るため,連続時間での極配置の直感を,離散時間の極配置(単位円との位置関係)へそのまま対応づけられます.
参考:Z変換/Z逆変換 頻出表
基本ペア
| 時間領域 \(x[n]\) | Z領域 \(X(z)\) | コメント |
|---|---|---|
| \(\delta[n]\) | 1 | 単位インパルス |
| \(u[n]\) | \(\dfrac{1}{1-z^{-1}}\) | 単位ステップ |
| \(a^{n}u[n]\) | \(\dfrac{1}{1-a z^{-1}}\) | 一次系の基本(極:z=a) |
| \(a^{n-1}u[n-1]\) | \(\dfrac{z^{-1}}{1-a z^{-1}}\) | 1サンプル遅れつき指数 |
| \((1-a^{n})u[n]\) | \(\dfrac{1}{1-z^{-1}}-\dfrac{1}{1-a z^{-1}}\) | 「立ち上がり」形で便利 |
変換の性質(計算で頻出)
| 性質 | 時間領域 \(x[n]\) | Z領域\(X(z)\) |
|---|---|---|
| 線形性 | \(\alpha x_1[n]+\beta x_2[n]\) | \(\alpha X_1(z)+\beta X_2(z)\) |
| 遅延 | \(x[n-m]\) | \(z^{-m}X(z)\) |
| 畳み込み | \((x*h)[n]\) | \(X(z)H(z)\) |
逆変換
| Z領域 \(X(z)\) | 時間領域 \(x[n]\) |
|---|---|
| \(\dfrac{A}{1-a z^{-1}}\) | \(A\,a^{n}u[n]\) |
| \(\dfrac{A z^{-1}}{1-a z^{-1}}\) | \(A\,a^{n-1}u[n-1]\) |
| \(\dfrac{A}{1-z^{-1}}\) | \(A\,u[n]\) |
まとめ
- 連続時間にラプラス変換があるように,離散時間の解析にはZ変換を用いる
- Z変換では (z^{-1}) が1サンプル(1クロック)遅延を表す
- 差分方程式をZ変換することで伝達関数 (H(z)) を得られる
- 安定性は極で決まり,極が単位円内((|p|<1))なら安定
- (z=e^{sT}) により,ラプラス変換の感覚を z 領域へ持ち込める