本記事は,アナログ・デジタル変換器(ADC)を題材に,筆者自身の理解を深める目的で整理している「ADC入門シリーズ」の一部です.シリーズ全体の方針や位置づけについては,以下の記事をご覧ください.
はじめに
前回の記事では,スイッチトキャパシタ(Switched Capacitor,以下 SC)回路の基本動作を整理しました.今回の記事では一歩進めて,SC 回路の回路解析に踏み込みます.
参考資料としている講義動画では,SC 回路を KCL(Kirchhoff’s Current Law,キルヒホッフの電流則)から導出し,理想条件のもとでは最終的に電荷保存の形に帰着することを示していました.SC 回路は電荷保存則で語られることが多く,定常値だけを求める目的であれば,そのアプローチで十分なことがほとんどです.
一方で,実際の回路には非理想要因が数多く存在します.たとえば,オペアンプの有限利得や出力電流制限,スイッチのオン抵抗,寄生容量などです.速度や帯域を議論する場合には,これらの影響によって過渡応答(settling)を無視できない場面も出てきます.そのため,「電荷保存だけ」で完結させる理解には限界があります.
今回の記事では,「電荷保存は理想条件下における KCL の簡約形にすぎない」という結論の元,SC 回路の定常値解析を KCL の視点で整理します.また,最後にはラプラス領域での考え方にも触れていきます.
前提条件
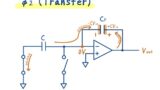
回路解析を行う上で,対象回路と,前提条件を確認しておきます.前回記事で扱ったものと同様に,下図のような SC アンプを考え,2相クロックでの動作を想定します.
- \(\phi_1\):容量 \(C\) が入力 \(V_{\text{in}}\) をサンプリングし,フィードバック側の容量 \(C_F\) をリセット
- \(\phi_2\):\(C\) に保持された電荷が \(C_F\) へ転送され,出力 \(V_{\text{out}}\) が決定
本記事で導出したいのは,\(\phi_2\)の終わりの \(V_{\text{out}}\) です.
今回の解析としては,参考文献の講義動画の内容と同様に理想条件を仮定します.
- 理想スイッチ(オン抵抗ゼロ,切替は瞬時)
- 理想オペアンプ(無限利得,入力電流ゼロ,仮想接地が成立)
- 寄生成分(オフ容量など)は無視
重要なのは,これらの前提によって電圧がクロック境界で瞬時にジャンプすることです.この性質が,後で KCL を電荷保存の形へ落とし込む鍵になります.
出力電圧(\(V_{\text{out}}\))の導出
前章の前提を踏まえ,時間領域で KCL を立てて順番に整理します.本章のポイントは,KCL を立てるノードを適切に選ぶことと,クロック切替時の電圧ステップを δ 関数で表現することです.
KCL を立てるノード
KCL は形式的には任意のノードに書けますが,未知量のあるノードに書くと式が閉じません.例えば出力ノードでは,オペアンプの出力電流が未知であるため,そのままでは扱いにくいです.
今回の回路では,仮想接地の入力ノードに KCL を立てるのが最も整理しやすいです.
ここで,\(i_1(t)\) をサンプリング容量 \(C\) を流れる電流,\(i_2(t)\) をフィードバック容量 \(C_F\) を流れる電流とすると,下式が成り立ちます.
\(i_1(t)+i_2(t)=0\)
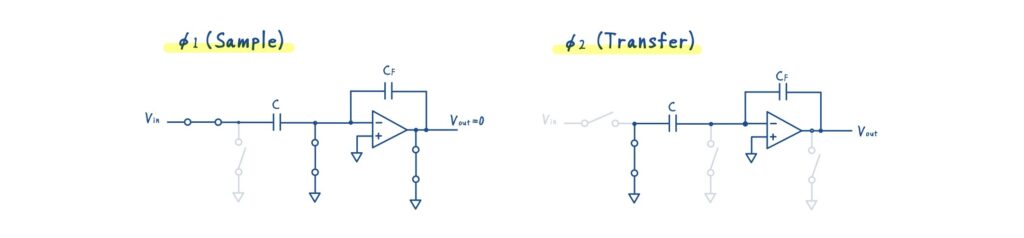
また電圧については,下図の極性で定義し,サンプリング容量の両端電圧を \(v_C(t)\),フィードバック容量の両端電圧を \(v_{CF}(t)\) とします.
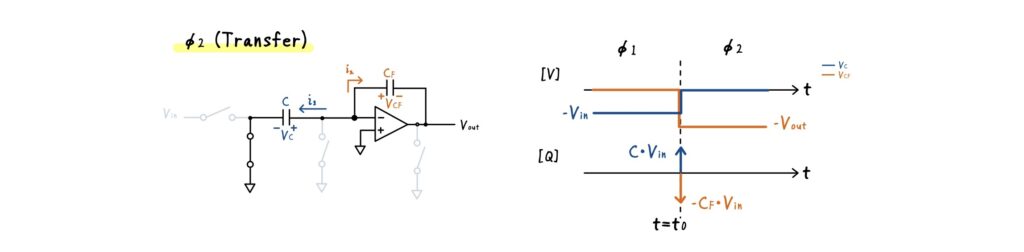
サンプリング容量 \(C\) の電圧 \(v_C(t)\)
クロック位相により,\(v_C(t)\) は次のように変化します.
- \(\phi_1\) の終わりでは,\(v_C=-V_{\text{in}}\)
- \(\phi_2\) に入る瞬間に,\(v_C = 0\) にジャンプ
このジャンプするタイミングである\(\phi_2\) 開始時刻を \(t=t_0\) として表すと,
\(v_C(t)= -V_{\text{in}} + V_{\text{in}}\,u(t-t_0)\)
となります(\(u(t)\) は単位ステップ関数).よって,
\(\frac{dv_C(t)}{dt}=V_{\text{in}}\,\delta(t-t_0)\)
です.したがって,サンプリング容量 \(C\) に流れる電流は,
\(i_1(t)=C\frac{dv_C(t)}{dt}=C\,V_{\text{in}}\,\delta(t-t_0)\)
となります.ここで δ 関数はクロック切替時刻(\(t_0\))に現れるインパルスです.また,係数 \(C\,V_{\text{in}}\) は,インパルスの面積に対応し,電荷変化 \(\Delta Q\) を表します.
フィードバック容量 \(C_F\) の電圧 \(v_{CF}(t)\)
同様に,\(C_F\) 両端電圧 \(v_{CF}(t)\) は次のように変化します.
- \(\phi_1\) ではリセットされて \(v_{CF}=0\)
- \(\phi_2\) に入ると \(v_{CF} = V_{\text{out}}\) にジャンプ
よって,
\(v_{CF}(t)= V_{\text{out}}\,u(t-t_0)\)
\(\frac{dv_{CF}(t)}{dt}=V_{\text{out}}\,\delta(t-t_0)\)
となります.今回は,KCL に入れる電流の向き(符号)は,仮想接地ノードから流出する向きで定義しています.符号は「どちら向きを正の電流と定義したか」に依存しますが,最終的に KCL で相殺する向きに統一します.本記事の定義では,
\(i_2(t)= -C_F\frac{dv_{CF}(t)}{dt}= -C_F\,V_{\text{out}}\,\delta(t-t_0)\)
と書けます.
KCL へ代入
以上より \(i_1(t)\),\(i_2(t)\) が求まったので,これらを はじめに定義した KCL の式(\(i_1(t)+i_2(t)=0\))に代入します.
\(C\,V_{\text{in}}\,\delta(t-t_0)\;-\;C_F\,V_{\text{out}}\,\delta(t-t_0)=0\)
\(\delta(t-t_0)\) をくくると,
\(\bigl(C\,V_{\text{in}}-C_F\,V_{\text{out}}\bigr)\,\delta(t-t_0)=0\)
となります.等式が成り立つためには,\(C\,V_{\text{in}}-C_F\,V_{\text{out}}=0\) なので,
\(V_{\text{out}}=\frac{C}{C_F}V_{\text{in}}\)
が得られます.これで,今回の解析対象回路の出力電圧が KCL によって求まりました.
前回の記事でも触れたように,この回路トポロジーの強みは,容量比 \(C/C_F\) によって利得を決定できる点にあります.
電荷保存則への帰着
ここは講義の核心のひとつで,「なぜ電荷保存と言えるのか」を原理側から整理します.
容量に流れる電流は,下式で与えられます.
\(i(t)=C\frac{dv(t)}{dt}\)
理想スイッチ,理想オペアンプの前提では,クロック切替で電圧がステップ状に切り替わります.ステップの微分はインパルスなので,電流は時間軸で見ると \(\delta\) 関数で表現できます.
ここで重要なのは,インパルスの「高さ」ではなく「面積」に物理的意味がある点です.実際,
\(\int i(t)\,dt = \int C\frac{dv(t)}{dt}\,dt = C\Delta v = \Delta Q\)
となり,インパルス電流の面積は電荷変化 \(\Delta Q\) に一致します.
前章で得られた \(C V_{\text{in}}-C_F V_{\text{out}}=0\) は,まさに \(\Delta Q_C+\Delta Q_{CF}=0\) を電圧で書き直した形になっています.
したがって,理想 SC 回路では,KCL の「電流の和=0」を時間積分することで,「電荷変化の和=0」として扱えます.この意味で,KCL が電荷保存へ簡約されると理解できます.
ここまでをまとめると,次の関係です.
- 集中定数回路の基本原理は KCL である.
- 理想スイッチ+容量の条件では,電流がインパルスになる.
- インパルスの面積は電荷変化なので,KCL は電荷保存の形に落ちる.
よって「SC だから電荷保存」ではなく,「理想条件下では KCL が電荷保存に見える」と理解しておくと,非理想要素を追加したときにも迷子になりにくくなります.
ラプラス領域
ラプラス領域の考え方も,同様に整理していきます.ラプラス領域では,あるノードについて,KCL を立てると,次のようになります.
\(\sum I_k(s)=0\)
ここで押さえたいのは,ラプラス変換の定義が時間積分 \(\int(\cdot)\,dt\) を含むため,電流 \(i(t)\) を変換した \(I(s)\) が A・s の次元を持つ,という点です.A・s は C(クーロン)であり,電荷 \(Q\) と同じ次元です.つまり,ラプラス領域で電流を扱うとき,式の中には電荷(時間積分した量)が自然に入り込んでいます.
ラプラス変換補足
ラプラス変換は,時間関数 \(x(t)\) を,複素数 \(s\) を変数とする関数 \(X(s)\) に写す変換で,下記のように定義されます.
\(X(s)=\mathcal{L}\{x(t)\}=\int_{0}^{\infty} x(t)e^{-st}\,dt \)
直感的には,\(e^{-st}\)(指数関数)を重みとして \(x(t)\) を積分し,時間波形 \(x(t)\) を「s による表現」へ写像している,と見なせます.
この変換を使うと,時間領域での微分が s による代数演算へ写るため,微分方程式を代数方程式として扱えるのが大きな利点です.代表的には,初期値を含めて
\(\mathcal{L}\left\{\frac{dx(t)}{dt}\right\}=sX(s)-x(0^-) \)
が成り立ちます.(本記事では,この性質を使って KCL をラプラス領域で書き直す,という位置づけになります.)
定常値(settled value)だけに興味があるとき,時間領域では \(t\to\infty\) を見ます.ラプラス領域では,これに対応するのが \(s\to0\) です.\(s=0\) を代入すると指数項が消え,
\(I(s=0)=\int i(t)\,dt\)
となります.右辺は電流の時間積分なので,そのまま電荷 \(Q\) です.したがって,「ラプラス領域で KCL を立て,定常値として \(s=0\) を評価する」という手順は,結局「ノードに出入りする電荷をそろえる」という意味で,電荷保存則と同じ内容を含んでいます.
一方で,非理想性を含む場合は,電荷保存則だけでは過渡の形まで決まりません.スイッチにオン抵抗 \(R_{\text{on}}\) が入ると,電圧は瞬時にジャンプせず,指数関数的に遷移します.過渡波形まで求めたい場合には,ラプラス変換で解いた解を時間領域へ戻す必要があり,そのために逆ラプラス変換(あるいは時間領域の微分方程式の解法)が必要になります.
ただし,「クロック期間内に十分 settle する」ことを前提とすれば,最終値だけが欲しいなら電荷保存(= KCL の簡約)で十分,という判断になります.
まとめ
本稿では,スイッチトキャパシタ(SC)回路の解析を題材に,「なぜ SC 回路は電荷保存で解けると言えるのか」を,原理である KCL から整理しました.結論として,理想条件のもとでは KCL が電荷保存の形に簡約されます.
ポイントを振り返ると,次のとおりです:
- 原理は KCL であり,電荷保存は理想条件下における KCL の簡約形として現れる.
- 理想スイッチ・理想オペアンプでは電圧がステップ状に切り替わり,容量電流は \delta 関数(インパルス)で表現できる.
- インパルス電流の面積は \(\int i(t)\,dt=C\Delta v=\Delta Q\) となり,KCL を時間積分すると「電荷変化の和=0」に帰着する.
- その結果,\(C V_{\text{in}}-C_F V_{\text{out}}=0\) から \(V_{\text{out}}=\frac{C}{C_F}V_{\text{in}}\) が得られ,利得は容量比で決まる.
- 非理想性(\(R_{\text{on}}\) など)を入れると過渡が支配的になり,波形まで求めるにはラプラス変換と逆変換が必要になるが,十分 settle する前提なら最終値は電荷保存で扱える.
以上です.最後まで読んでいただきありがとうございました.
参考文献
記事はあくまで筆者の勉強備忘録のため,より正確に理解したい,さらに深く理解したい場合は下記をご参照ください.
- IIT Kanpur: https://www.iitk.ac.in
- SSCD Lab: https://iitk.ac.in/sscd
- 講義動画(YouTube): https://youtu.be/cI7bYpW7EvE?si=uhuL8tSMJan23LHf
- 『アナログ/デジタル変換入門 ― 原理と回路実装 ―』 和保孝夫(監)/コロナ社
- 『ΔΣ型アナログ/デジタル変換器入門 第2版』 和保孝夫・安田彰(監訳)/丸善出版
- 『アナログCMOS集積回路の設計 応用編』Behzad Razavi(著),黒田忠弘(監訳)/丸善出版
ー 第12章 スイッチトキャパシタ回路 ー - 『CMOSアナログ回路入門』 谷口研二(著)/CQ出版社
ー 第15章 スイッチト・キャパシタ ー

(ADCの基礎を一通り確認する目的で,最初の一冊として取り組みやすい内容です.価格も,専門書の中では比較的手に取りやすいと思います.)

(筆者が所持しているのは第 1 版ですが,こちらも分かりやすくておすすめです.)
スイッチトキャパシタについては,下記2冊が分かりやすいです.