本記事は,アナログ・デジタル変換器(ADC)を題材に,筆者自身の理解を深める目的で整理している「ADC入門シリーズ」の一部です.シリーズ全体の方針や位置づけについては,以下の記事をご覧ください.
はじめに
前回の記事では、DFT(離散フーリエ変換)を使って信号を周波数領域へ変換する方法を学びました。今回はその続きとして、実際にADCを評価する際に避けて通れない現象であるスペクトルリーケージ(Spectral Leakage)について解説していきます.
スペクトルリーケージは,前回の記事でも触れたように,信号を有限長に切り取ってDFTを行うことによる副作用です.DFTでは,有限区間の信号を周期的に繰り返すと仮定するため,切り取り方によっては区間の端点で不連続が生じる場合があります.この時間領域での不連続が,周波数領域ではスペクトルリーケージとして現れます.
今回は,時間領域で端点の不連続がなくなるように,端に行くほど0に近づくような窓関数をかけることで,時間信号をなめらかに処理する方法を学びます.
スペクトルリーケージ(Spectral Leakage)
DFTは,入力信号を周期的に繰り返されるものとして扱います.
つまり,有限長 N サンプルの信号をコピーして左右に無限に貼り付けた状態を想定しているのです.
前回の記事で学んだように,有限区間が信号のちょうど整数周期で切り取られていれば,端点同士が滑らかにつながります.そのため,周期的に並べてもギャップがなく,理想的な正弦波が連続します.
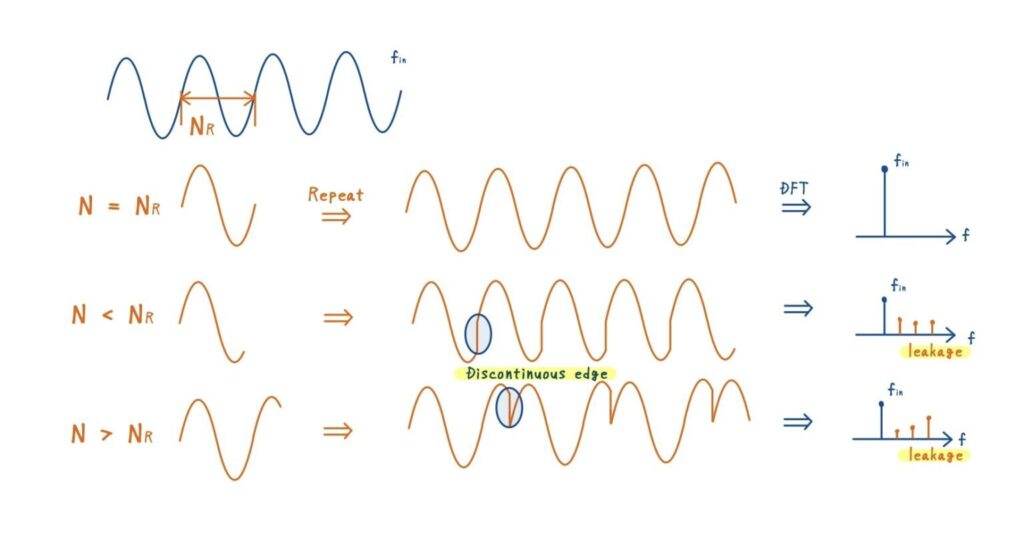
しかし,もし信号が途中で切れていたり,あるいは複合的な周期成分を含んでいる場合(たとえば2つ以上の正弦波が混ざった入力など)には,サンプルの端点が必ずしも一致しません.
その結果,周期拡張した際に不連続なジャンプが生じます.この不連続な点は時間領域ではインパルス的な誤差として現れ,その誤差は周波数領域では広帯域なフラット成分になります.
つまり,端点の不連続 = 時間領域のジャンプ = 周波数領域のリーケージという関係です.
リーケージは,信号が複雑な形になるほど顕著になります.三角波やパルス列のような複雑な波形は,多数の周波数成分を含むため,それぞれの成分が観測窓に対して非整数周期となりやすく,結果としてリーケージが強く現れます.したがって,単一のサイン波だけでなく,実際の信号のほとんどでリーケージは避けられません.
窓(ウィンドウ)関数
スペクトルリーケージの対策として,有効なのが窓関数(Window Function)です.
窓関数とは,端点の不連続点をなめらかにするため,信号の両端を少しずつ弱めるように重みづけされた関数です.
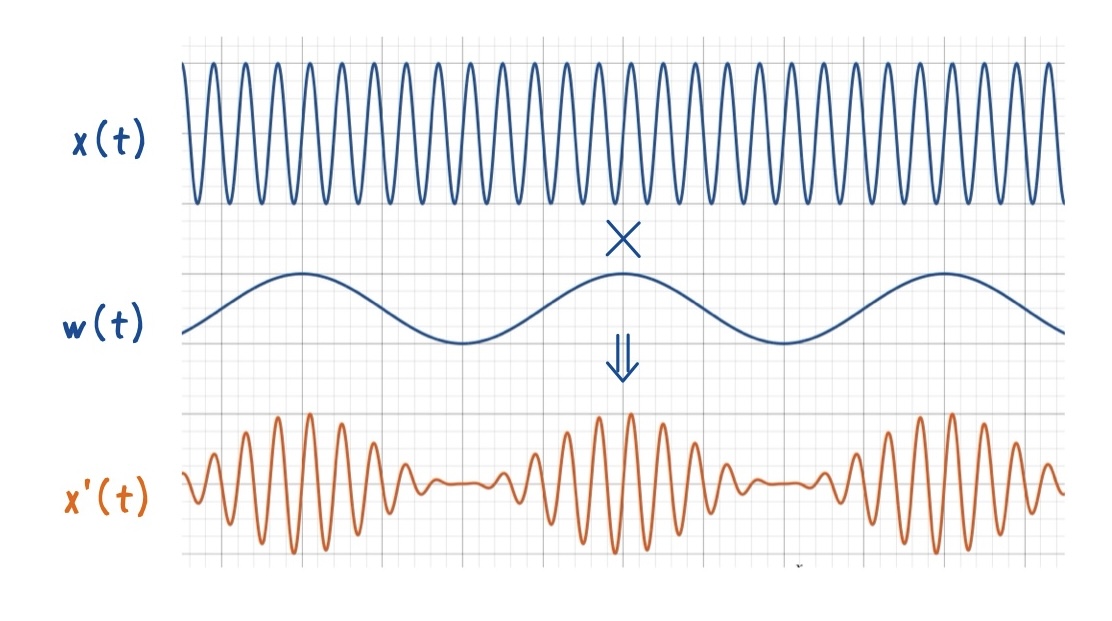
窓を掛ける処理は,概念的に次の3ステップになります.
1.無限長の信号を N サンプルで切り取る(=矩形窓を掛ける)
2.端がなめらかになるように窓関数 w[n] を掛ける
3.その結果をDFTにかける
図にイメージを書きました.この操作により,端点は不連続点がなくなり,なめらかに繰り返します.その結果,スペクトルリーケージが大幅に減少します.
Hann(ハン)ウィンドウの定義と性質
代表的な窓関数のひとつが Hann(ハン)窓 です.その定義は次の式で表されます.
\(w[n] = \frac{1}{2}\left(1 – \cos\!\left(2\pi \frac{n}{N}\right)\right)\)
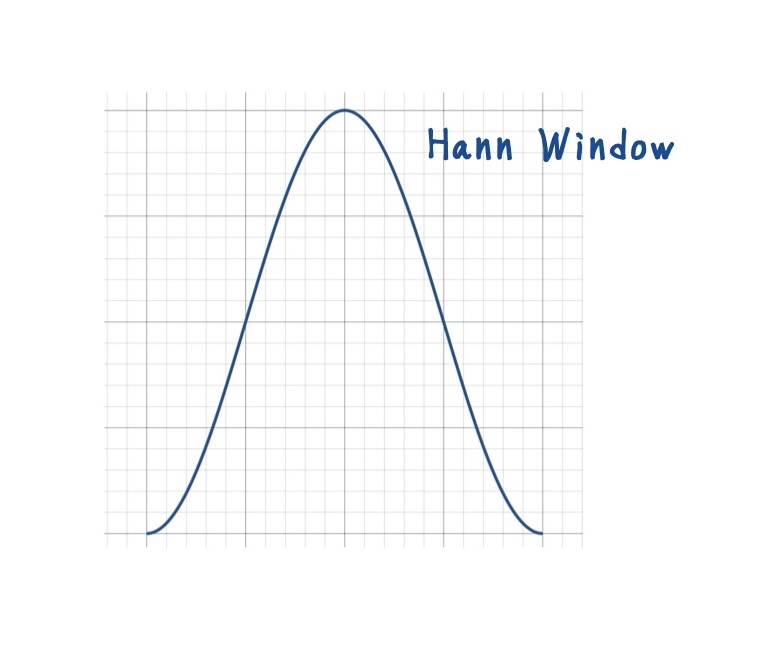
この式は余弦関数を基にしており,中央で 1,両端で 0 となるよう設計された滑らかな曲線です.時間領域では端点が緩やかに 0 に近づくため,周期的に拡張しても不連続が生じません.
Hann 窓を掛けた信号は次のように表されます.図は離散化していませんので,イメージを掴む程度の参考情報です.
\(x’[n] = x[n] \cdot w[n]\)
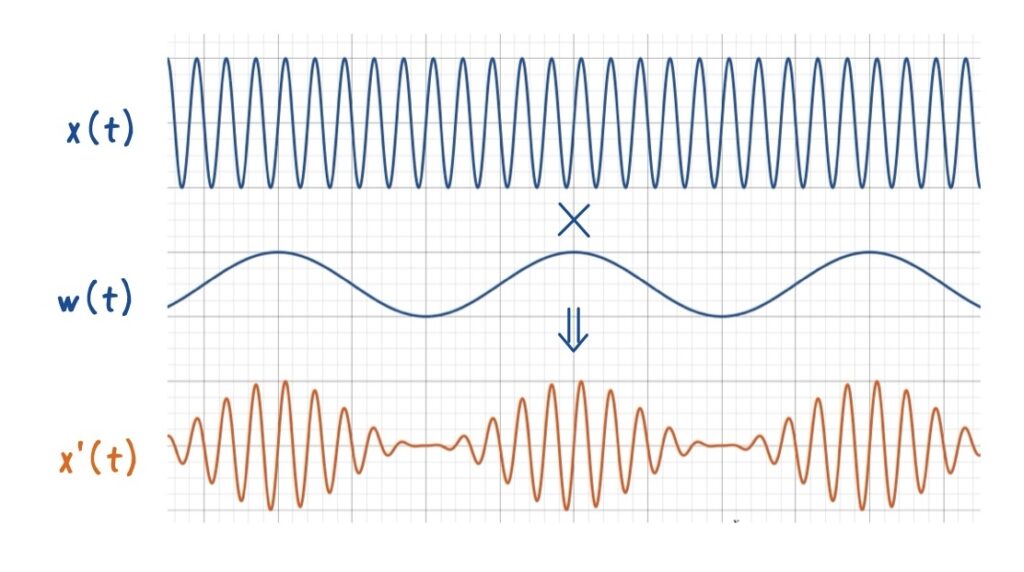
中央部の信号はほぼそのまま残り,端に近づくにつれて徐々に重みが小さくなるため,信号を周期的に並べても滑らかに接続されます.その結果,ビンにのっていない信号であってもスペクトルリーケージを大幅に低減できます.
(余談です.講義内では “lying on a bin” という表現がたびたび登場します.あまり馴染みのない言葉で自信がないのですが,本記事では便宜上「ビンにのる」と訳しています.これは,時間領域におけるサンプル数 N と信号の周期が整数倍の関係にある状態を指します.)
窓関数の副作用
ここまで,窓関数によるスペクトルリーケージの抑制効果を書きました.しかし,窓掛け処理は万能ではありません.端点をなめらかにすることでリーケージは減りますが,同時にいくつかの副作用が生じます.講義の中でもこの「トレードオフ」について再三強調されており,この副作用について理解しておくことは,周波数特性を正しく扱うためには必要です.
3-1 信号パワーが小さくなる
まず第一に窓関数を掛けると,全体のパワーが減少します.これは端になるほど信号を弱めている(=エネルギーを小さくしている)ため,物理的にも自然な結果です.数式で確かめてみましょう.
ここでは,入力信号を単純なコサイン波とします.
\(x[n] = \cos\!\left(2\pi \frac{M}{N}n\right)\)
これにHann窓
\(w[n] = \frac{1}{2}\left(1 – \cos\!\left(2\pi \frac{n}{N}\right)\right)\)
を掛けると,
\(\begin{aligned} x’[n] &= x[n] \cdot w[n] \\ &= \frac{1}{2}\cos\!\left(2\pi \frac{M}{N}n\right) – \frac{1}{4}\cos\!\left(2\pi \frac{M+1}{N}n\right) – \frac{1}{4}\cos\!\left(2\pi \frac{M-1}{N}n\right) \end{aligned}\)
という3つの成分に分解されます.つまり,本来は1つであった余弦波のピークが,窓関数を掛けることによって3つに分かれるのです.
振幅比は 1/2:1/4:1/4なので,これらの成分のパワーを合計すると,
\(P_\text{Hann} = \frac{(1/2)^2}{2} + \frac{(1/4)^2}{2} + \frac{(1/4)^2}{2} = \frac{3}{16}\)
一方,窓なしの信号パワーは \(P_\text{orig} = 1/2\) なので,
\(\frac{P_\text{Hann}}{P_\text{orig}} = \frac{3/16}{1/2} = \frac{3}{8}\)
つまり,Hann窓を掛けるとパワーは元の3/8に低下します.
ここで注意が必要なのが,SNR(信号対雑音比)を計算する場合は,このパワー低下は特に問題になりません.信号も雑音も同じウィンドウを掛けるため,平均化の\(\frac{1}{N}\) や パワー係数の\(\frac{8}{3}\) は分子・分母で相殺されます.しかし,絶対値としての電力や実効値を求めたい場合には要注意です.窓を掛けた分だけエネルギーが減っているため,正確に戻すには補正が必要です.
Hann窓の場合,パワーが3/8倍になっているので,電力を求める際は \(\times \frac{8}{3}\) を掛けて補正します.
\(P = \frac{8}{3} \cdot \frac{1}{N} \sum_{k=M-1}^{M+1} S_V[k]\)
3-2 周波数分解能の低下
もうひとつの副作用は,分解能の低下です.前の章で解いた式から分かるように,Hann窓を掛けると,1本の周波数成分が3ビンに広がります.つまり,隣接する周波数を分離する能力が3分の1に下がるということです.同じ分解能を確保したい場合は,DFTの点数 N を増やす必要があります.
このように,Hann窓はリーケージを大きく減らせますが,その代わり,
- 信号パワーが小さくなる(Hann窓は3/8倍)
- 周波数分解能が悪くなる(Hann窓は3ビンに拡がる)
という代償があります.
“信号パワーが減少する”・”周波数分解能が低下する”といった副作用はその他の窓関数にも共通して言えることです.なめらかにすればするほど,リーケージは抑制できますが,同時にこういった副作用が顕著になってきます.
このトレードオフを理解して使うことが,正しいFFT解析の第一歩です.
ブラックマン・ハリス窓(Blackman–Harris)
Hann窓を用いることでリーケージは大きく抑えられることが分かりましたが,それでも主ピークの両側に小さなサイドローブ成分が残ることがあります.これをさらに低減するために用いられるのが,より滑らかなブラックマン・ハリス(Blackman–Harris)窓です.この窓について解説していきます.
なお,先生も講義で言っていましたが,DSPの教科書を開けば窓関数は山ほど載っています.たとえば,以下のようなものが代表的です.
| 種類 | 数式の特徴 | 特徴・用途 |
|---|---|---|
| Rectangular(矩形) | 全区間で1 | トランケートそのもの.リーケージ最悪だが分解能最高. |
| Hamming(ハミング) | 0.54 − 0.46cos(2πn/N) | Hannに似るが端点を完全に0にしない.音声解析などでよく使われる. |
| Blackman | 0.42 − 0.5cos(2πn/N) + 0.08cos(4πn/N) | Hannより滑らか.リーケージ小. |
| Blackman–Harris | 0.35875 − 0.48829cos(2πn/N) + 0.14128cos(4πn/N) − 0.01168cos(6πn/N) | 高精度評価やADC測定で定番. |
このように窓関数の種類は多いのですが,アナログ回路設計者の立場からすれば,実務上はHann窓とBlackman–Harris窓の2種類を理解していれば十分だと思います.
ブラックマン・ハリス窓の特徴
Blackman–Harris窓は,Hann窓よりも端をさらに滑らかに落とすことで,リーケージをさらに小さく抑えます.
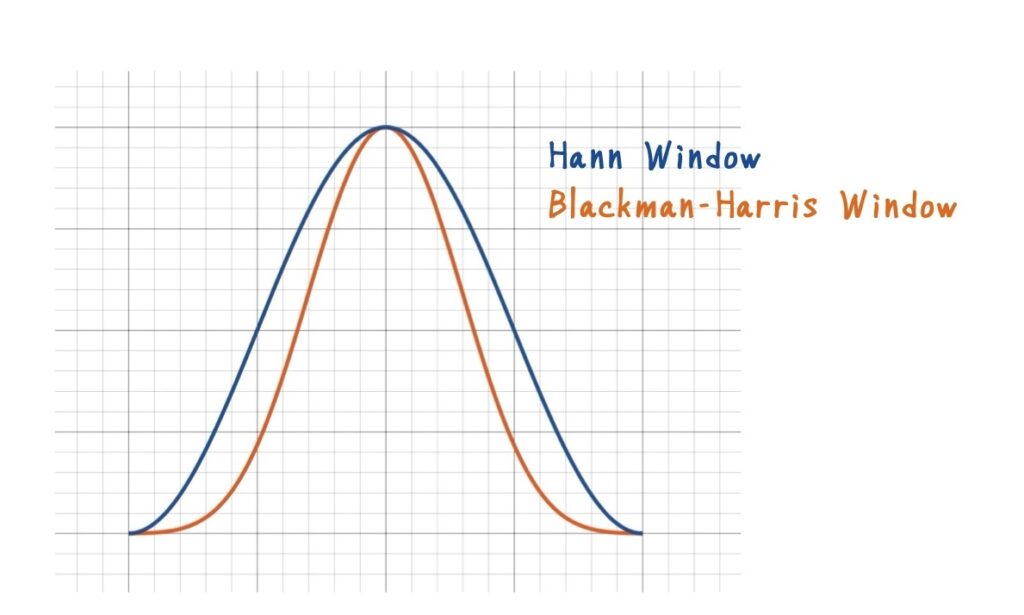
一方で,そのぶんパワーが減り,ピークがより広がるという代償を払います.
| 特徴 | Hann窓 | Blackman–Harris窓 |
|---|---|---|
| 数式形状 | 1項(cos) | 3項(cos³まで) |
| 端の滑らかさ | 中程度 | 非常に滑らか |
| リーケージ抑制 | ◎ | ◎◎(さらに強力) |
| スピルビン数 | 3(中心±1) | 7(中心±3) |
| 信号パワー | 元の3/8 | さらに小さい(およそ0.33倍) |
| 分解能 | 中 | 低(ピークが広い) |
| 用途 | 一般的なFFT評価 | 高精度ADCやノイズ特性測定など |
Hann窓のスペクトルは中心±1ビン(合計3ビン)に広がるのに対し,Blackman–Harris窓では中心±3ビン(合計7ビン)の範囲に分散します.その分,サイドローブ(横の尾)は非常に低く,にじみがほとんど見えません.
Hann窓とBlackman-Harris窓を比較して分かるように,窓関数を滑らかにすればするほど,リーケージは確かに減ります.しかし,同時に信号のパワーも分解能も落ちていきます.
つまり,どの窓関数を使うかは目的に合わせて正しく選ぶことが大事です.例えば,信号の形やノイズフロアをざっくり把握したいのならば,Hann窓で十分ですし,高精度にSNRを測定したいとなれば,Blackman-Harris窓が好ましいです.
測りたい指標(SNか分解能か)に応じて窓を選ぶという視点が大切ということです.
実務での扱い
ここまでで,窓掛け処理の原理とトレードオフを理解しました.では,この窓掛け処理を実務でどのように使い分けるべきでしょうか.講義内では「シミュレーションと実測の場合の使い方」について次のように説明がありました.
まず,シミュレーションの場合です.シミュレーションでは入力信号の周波数を自由に設計できるため,入力信号がちょうどDFTのビン上に一致するように設定すれば,端点での不連続が発生せず,リーケージは理論的に生じません.この場合,ウィンドウ関数を用いる必要はありません.
一方,実測では入力周波数を厳密に制御することができないため,端点の不連続が必ず生じます.そのため,FFT解析を行う際にはHann窓やBlackman–Harris窓などの窓関数が用いられます.
実務目線での補足
ただし,ここで少し誤解が生じやすいポイントがあります.講義内で「シミュレーションでは \(f_{in} = M/N \times f_s\) に設定すればよい」と説明されていましたが,ここでの“シミュレーション”とは,おそらく理論シミュレーションを指しているかと思います.
例えば,理想素子のみで構成されたアーキテクチャレベルの実装において,理論的なENOBやSNRを計算する場合には,確かにウィンドウ処理は不要です.入力信号とサンプリングクロックを完全に同期させられるため,端点が連続し,リーケージは発生しません.
回路設計レベル(トランジェント解析)
一方,アナログ回路設計の現場で行う特性解析シミュレーション(SPICEトランジェント解析)では状況が異なります.この場合,入力信号がサンプリング周波数と完全に同期するとは限らず,回路の非線形性による歪み成分や,クロックジッタなどの要因によって整数周期ではない成分が混入します.その結果,DFTやFFTを実行すると端点不連続が発生し,実測と同様にスペクトルリーケージが現れます.
したがって,この場合は窓関数を使用することが推奨されます.
例えば,VirtuosoなどのEDAツールでFFT解析を行う際には,解析設定内に「Window Type」というプルダウン項目があります.ここでは下図に表示したように窓関数を選択することができます.見慣れない Kaiser窓 や Parzen窓 なども含まれていますが,一般的な特性評価であれば,Hann窓 あるいは Blackman–Harris窓 を選択しておけば無難です.
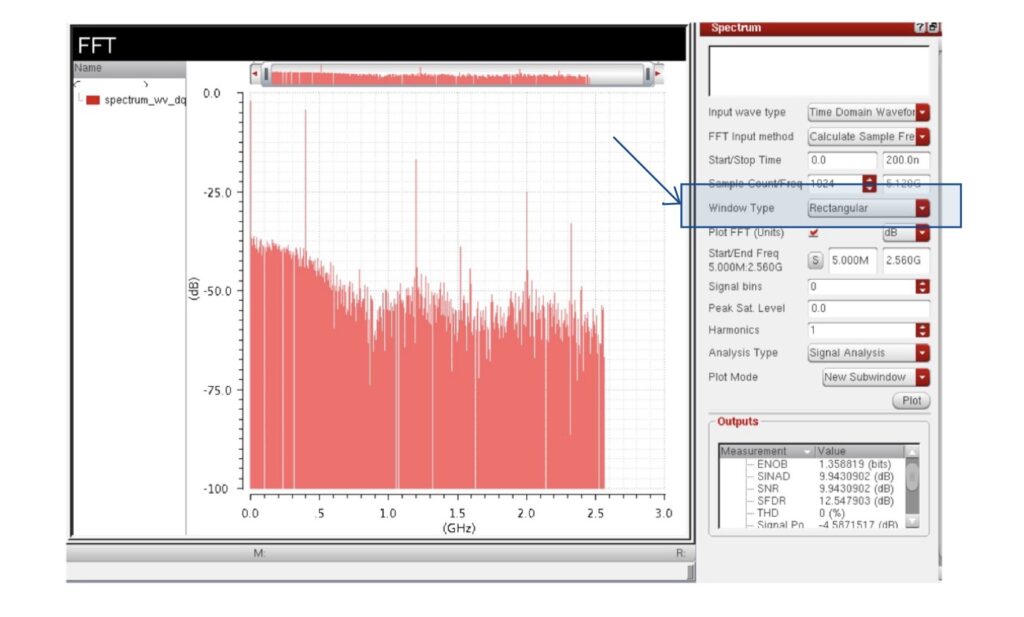
ノイズシェーピングADC
ここまでで,シミュレーションと実測におけるウィンドウの扱い方を整理しました.講義では,このほかに「ノイズシェーピングADC(ΣΔ型ADCなど)はまた特別な扱いになる」との説明もありました.
この部分については,筆者自身まだ十分に咀嚼できておらず,現時点では自信をもって解説できる段階にはありません.しっかり理解を深めてから別記事で丁寧にまとめたいと思います.
この辺り正しく理解できるよう,引き続き勉強に励んでいきます.
まとめ
本稿では,FFT解析で避けて通れない現象であるスペクトルリーケージと,その対策として用いられる窓関数について学びました.有限区間で信号を扱う以上,端点の不連続によるリーケージは必ず発生します.そのため,時間軸で信号をなめらかに処理する「窓関数」を掛けることが有効です.
ポイントを振り返ると次のとおりです:
- 端点の不連続がスペクトルリーケージの原因となる.
- Hann窓を用いるとリーケージを大きく低減できるが,信号パワーが3/8に低下し,分解能も悪化する
- Blackman–Harris窓はさらに強力にリーケージを抑えるが,パワー・分解能の低下が大きい
- 実務では,HannとBlackman–Harrisの2種類を使い分ければ十分
シミュレーションや実測でのFFT解析では,なぜ窓を掛けるのかを理解しておくことが重要です.理論上は不要な処理でも,実際の回路シミュレーションや測定環境では必須となります.
以上です.最後まで読んでいただきありがとうございました.
雑記:
Virtuosoを使って実際のFFT解析を解説したいなと思っているのですが,プライベート環境ではライセンス費用の都合でなかなか難しく...業務では日常的に使っているものの,さすがに個人利用には転用できませんし.無料で使えるEDAツールで代替できるか,いろいろ試してみようか検討中です.
参考文献
本記事はあくまで筆者の勉強備忘録のため,より正確に理解したい,さらに深く理解したい場合は下記をご参照ください.
- IIT Kanpur: https://www.iitk.ac.in
- SSCD Lab: https://iitk.ac.in/sscd
- 講義動画(YouTube): https://youtu.be/cI7bYpW7EvE?si=uhuL8tSMJan23LHf
- 『アナログ/デジタル変換入門 ― 原理と回路実装 ―』 和保孝夫(監)/コロナ社
- 『ΔΣ型アナログ/デジタル変換器入門 第2版』 和保孝夫・安田彰(監訳)/丸善出版

(ADCの基礎を一通り確認する目的で,最初の一冊として取り組みやすい内容です.価格も,専門書の中では比較的手に取りやすいと思います.)

(筆者が所持しているのは第 1 版ですが,こちらも分かりやすくておすすめです.)