離散フーリエ変換（DFT）とは？DTFTとの違いを解説

はじめに
フーリエ解析の種類を整理
入力信号の有限化
周波数領域の離散化
DFTの点数Nの意味と範囲の決め方
まとめ
参考文献

はじめに

前回の記事では，ADCの性能指標であるSQNRやENOBについて学びました．その中で，「信号と雑音の大きさを比べる」ためのパワースペクトル密度（PSD）が登場しましたね．

はじめに前回の記事では，ADCの性能を示すための重要な指標であるSQNRとENOBについて学びました．量子化によって信号がどれだけ劣化するのかを数値で表すこの指標は，ADC性能の根幹をなす重要な要素です．今回はそのSQNRの式をもう一度振り...

今回のテーマは，そのPSDを得るための前提となる離散フーリエ変換（Discrete Fourier Transform：DFT）です．
フーリエ解析には多くの種類があり，名前が似ていて混乱しやすい部分です．そこで本稿では，フーリエ解析の種類と性質を整理し，ADCシステムにおける役割を再確認します．
数式だけでなく，図を交えて直感的に理解できるよう構成しました．

フーリエ解析の種類を整理

ここで一度，「フーリエ〇〇」という言葉を整理しておきましょう．講義でもたびたび登場しましたが，それぞれの定義は断片的に触れられることが多く，全体像をつかみにくいと感じました．そこで本章では，ADCの目的とフーリエ変換の役割について筆者自身の理解を書き下ろします．

フーリエ解析とは，複雑な信号を単純な周波数成分に分解するための手法です．
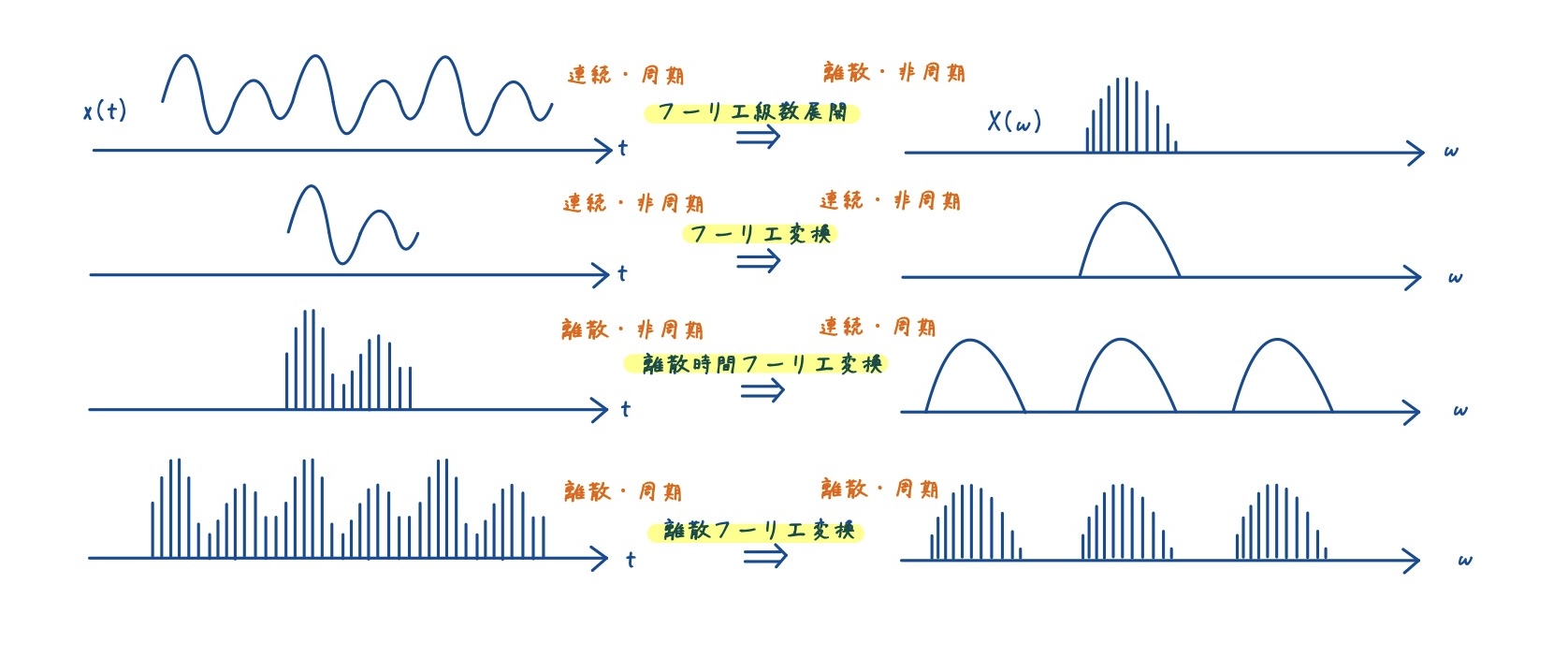
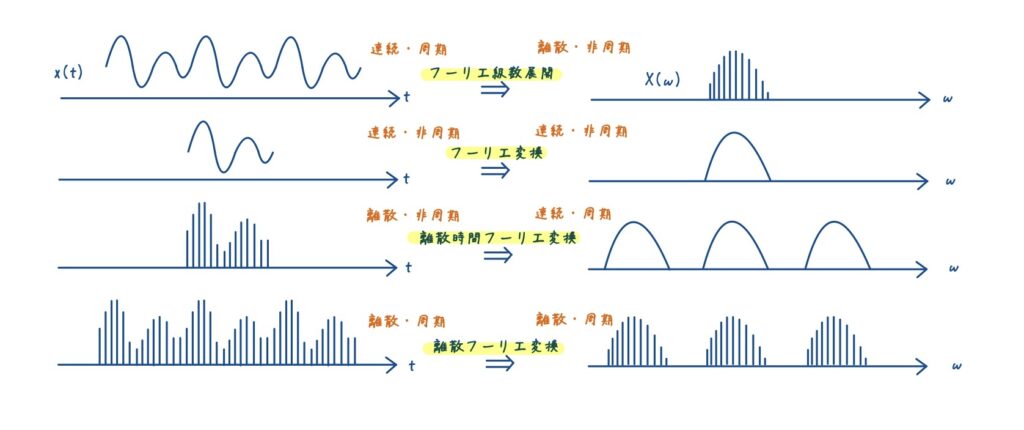
主な解析手法は次の4つであり，時間軸・周波数軸それぞれの連続性と周期性で分類されます．

名称	時間領域の性質	周波数領域の性質
フーリエ級数展開	連続・周期	離散・非周期
フーリエ変換	連続・非周期	連続・非周期
離散時間フーリエ変換（DTFT）	離散・非周期	連続・周期（2π周期）
離散フーリエ変換（DFT）	離散・周期（N点周期）	離散・周期（2π周期）

対応する定義式を示します：

\(\text{(1) フーリエ級数展開:}\quad x(t) = \sum_{k=-\infty}^{\infty} c_k e^{j k \omega_0 t}\)

\(\text{(2) フーリエ変換:}\quad X(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi f t} dt\)

\(\text{(3) 離散時間フーリエ変換(DTFT):}\quad X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}\)

\(\text{(4) 離散フーリエ変換(DFT):}\quad X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}\)

ADCとフーリエ解析の関係

次に，システムにおけるADCでの役割を振り返ります．
ADCでは，入力されたアナログ信号をコンピュータが扱えるデジタル信号へ変換します．ここで言う”扱える”とは，有限ビット(0/1)で表現できることでしたね．

ADCブロックから出力されたデジタル信号は，抽出や復号等，様々な処理が必要になります．
それらの処理は周波数領域で考えた方が直感的であり，効率が良いため，フーリエ解析によって周波数領域へ変換されます．

現実世界の信号は左上（連続・非周期）に位置し，コンピュータで扱いたいのは右下（離散・周期）の信号です．
左上から右下へ一気に変換できれば理想的ですが，数学的には不可能です．したがって，実装上の工夫として「①離散化」と「②有限化」を段階的に行う必要があります．この工夫によって，理論上の連続変換をコンピュータ上で再現可能にします．

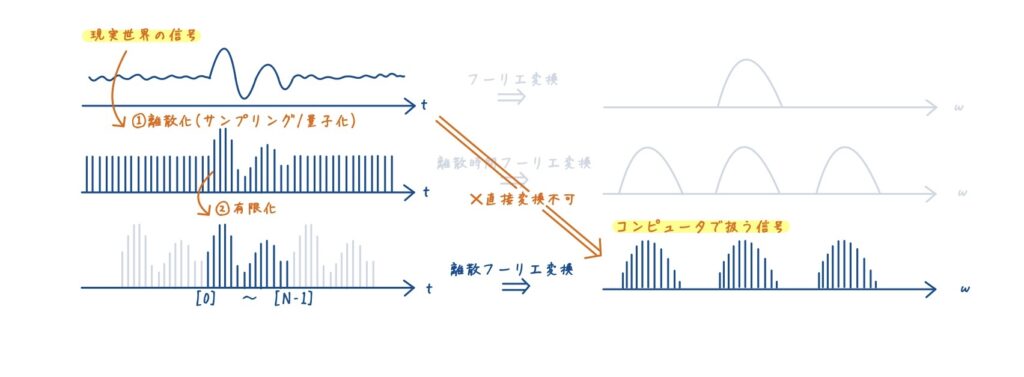
ADCのブロックでは，サンプリングと量子化によって「①離散化」を行います．しかし，この離散化だけでは不十分です．信号はまだ無限に続く非周期信号であり，そのまま離散時間フーリエ変換（DTFT）を行うと，周波数スペクトルは連続になります．DTFTは理論上の変換であり，無限長データを扱うことはコンピュータでは不可能です．
そこで次の処理②として，入力信号を有限化する必要があります．有限化によって離散フーリエ変換（DFT）が実装可能となり，初めて離散化された周波数スペクトルが得られます．

なお，この有限化には，後で登場する窓関数処理も含まれます．通常，これらの処理はADCではなく後段のDSPブロックで実装されます．そのため，アナログ回路設計者が有限化の実装を直接担うことはほとんどありません．しかし，ADCで設計した回路特性をシミュレーションや評価で解析する際には，この有限化の知識が欠かせません．正しく理解しておくことが重要です．

入力信号の有限化

サンプリングと量子化によって時間軸はすでに離散化されていますが，この段階では信号はまだ無限に続く非周期信号です．この信号を離散時間フーリエ変換（DTFT）すると，得られるスペクトルは依然として連続です．

\(X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}\)

理論的には美しい式ですが，無限長のデータをコンピュータで扱うことはできません．
そこで次のステップとして行うのが，有限化です．離散信号をN点だけ抜き出し，その範囲を解析対象とします．この操作によって，積分で表されていたフーリエ変換が「総和」に置き換わり，実装可能な形になります：

\(X[k] = \sum_{n=0}^{N-1} x[n] e^{-j\frac{2\pi}{N}kn}\)

有限化とは，サンプリングされたデータ列から必要な区間を切り取る操作です．この切り出し処理を数学的に見ると，信号にN点の矩形窓を掛けることと等価です．

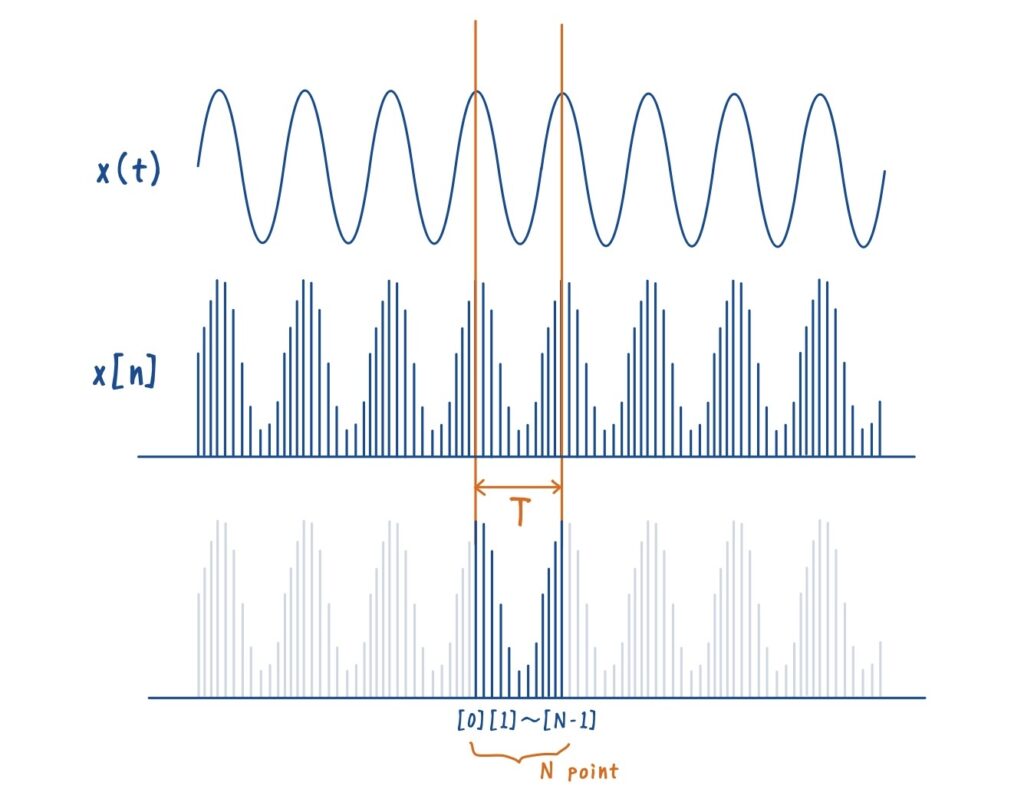
講義で示された正弦波を例に挙げます．正弦波は本来無限に続く波形ですが，サンプリング後の離散列の中からN点（[0], [1], [2], …, [N−1]）だけを抜き出すと考えます．その区間外のデータは窓によって0となり，解析対象から外れます．これにより，コンピュータ上で扱える有限データ列が得られるのです．

このように，DTFTでは無限に続く信号の積分を考えていましたが，区間が有限のデータ列になったことで，総和で示すことができます．こうして得られるのがDFTであり，時間を有限区間（N点）に制限することで，周波数軸を離散化して，N点分のスペクトルを得ることが式から分かります．

周波数領域の離散化

DFT後の周波数領域での特性を確認していきます．
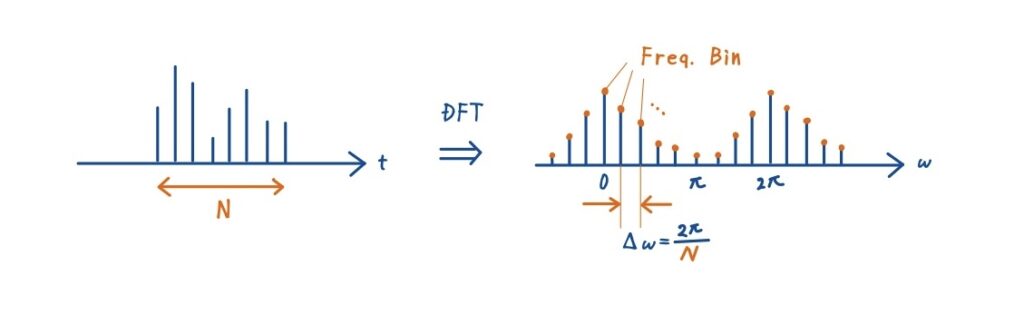
有限長信号をDFTで変換すると，周波数軸は離散的な点列として現れます．
その点間隔は次式で表されます．

\(\Delta \omega = \frac{2\pi}{N}, \qquad \Delta f = \frac{f_s}{N}\)

各点は周波数ビン（frequency bin）と呼ばれ，k番目のビンに対応する周波数は次の通りです．

\(\omega_k = \frac{2\pi k}{N}, \qquad f_k = \frac{k f_s}{N}\)

観測時間 \(T = N / f_s\) とすれば，

\(\Delta f = \frac{1}{T}\)

とも書けます．観測時間 T を長くすれば（＝Nを増やせば）分解能が上がり，短くすれば粗くなります．つまり，時間軸を有限化したことによって周波数軸が離散化されるわけです．
ここでいう「分解能」とは，隣接する周波数ビンの間隔 \(\Delta f\) のことであり，周波数分解能の物理的尺度を示します．

サンプリングと有限化の対応関係を整理すると，次のようになります．

操作	時間軸の変化	周波数軸の変化
サンプリング	離散化（周期 \(f_s\)）	帯域制限（\(\sim f_s/2\)）
有限化	区間制限（N点）	離散化（間隔 \(\Delta f = f_s/N，＝2\pi\)をN分割）

DFTの点数Nの意味と範囲の決め方

DFTでは，信号をN点に区切って解析することがわかりました．では，N点の範囲や決め方について，もう少し追っていきます．

DFTでは，計算の定義そのものから時間列が周期 N で繰り返すように“仮定”されます．

\(x[n+N] = x[n]\)

ここで重要なのは，実際にコンピュータが信号をコピーして繰り返しているわけではないということです．あくまで数学的な仮定として，「有限区間のデータが周期的に続いているように考える」だけです．

なぜそんな仮定を置くのかというと，フーリエ変換の性質上，時間領域で周期性を持たせることで，周波数領域を離散化できるからです．これはフーリエ変換の時間を「有限化すると，周波数が離散化される」という双対性の一つです．

この周期仮定により，逆変換の際にも整合性が保たれます．

\(x[n+N] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j(2\pi k / N)(n+N)} = x[n]\)

したがって、有限化された信号を解析するためには、時間領域で“繰り返されているように扱う”必要があるのです。

実際の信号周期と対応した切り取り区間を \(N_R\) とすると，次の3つのケースに分類できます．

下図のように，信号の周期と有限区間がぴったり一致していれば問題ありません．しかし，そうでない場合には，区間端で信号が不連続となり，急激な値の変化が生じます．この不連続が周波数領域に広がりを生み，本来の信号周波数以外の成分が現れてしまいます（＝スペクトルリーク）．

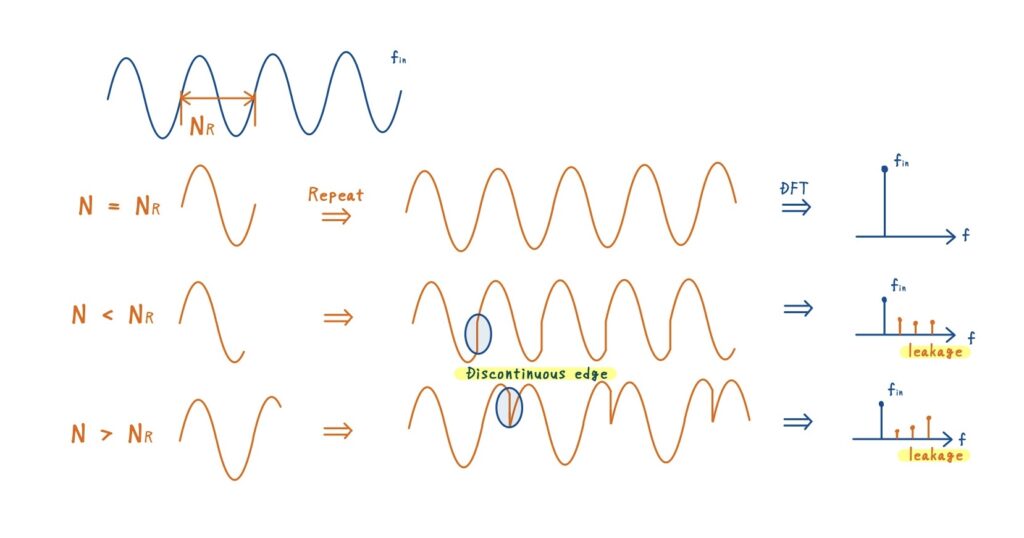
条件	状況	スペクトルの見え方
\(N = N_R\)	ちょうど整数周期分	単一ピーク（リークなし）
\(N < N_R\)	途中で切れている	リーク発生
\(N > N_R\)	整数周期を超える	リーク発生

このことから分かるように，有限化する切り取り区間は，本来は信号周期と一致していることが望ましいです．しかし，実際のアプリケーションでは，入力信号の周期そのものが未知である場合がほとんどです．そのため，切り取り区間を信号周期にぴったり合わせることは現実的には困難です．
この問題を補うのが，次回紹介する「窓関数」の考え方です．
信号の端点を滑らかに処理し，周期が一致しない場合でもリークを抑えることができます．