ADC入門 -SQNR・ENOB-

未分類

はじめに

前回の記事では，アナログ信号の物理量を離散的に扱うための「量子化」について整理し，その中で量子化誤差のモデル化を学びました．

ADC勉強会 -量子化-
はじめにアナログ信号をデジタルで扱うためには，入力された連続信号を離散化する必要があることを前回までに説明しました．時間軸方向を離散化するサンプリングについて学びましたが，離散化が必要なのは時間軸だけではありません．今回のトピックである量子...
nanaloglab.com
2025.10.04

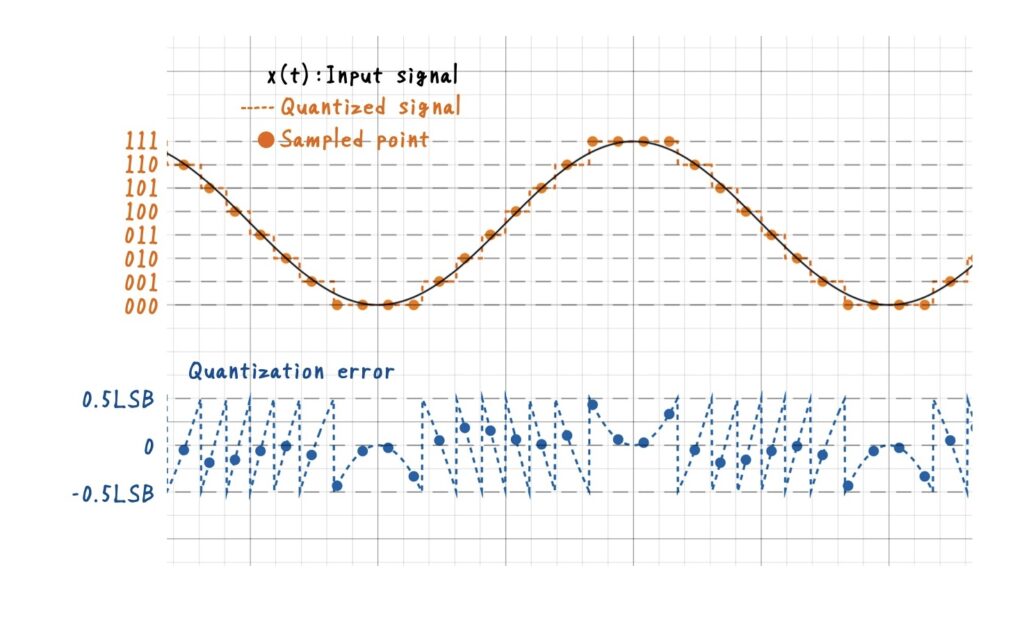
量子化とは，連続的な振幅を有限の目盛り（ビット）に丸め込む操作でしたね．入力信号を最も近い量子化レベルに割り当てる過程で，「誤差（Quantization Error）」が生じることを学びました．前回はこの誤差を，入力に依存する決定論的な誤差として考え，その後，解析を容易にするために確率的モデル（量子化ノイズ）で近似できることまで解説しています．

今回は，この量子化によって生じる誤差を定量的に評価するための指標であるSQNR（信号対量子化ノイズ比） と ENOB（実効ビット数） について整理します．

評価指標の必要性

量子化を学び，アナログ信号を有限ビットにすることで量子化誤差は不可避なことが分かりました．どんなに高精度なADCでも，ビット数が有限である限り，この誤差(あるいはノイズ)はゼロにはなりません．
だからこそ，私たちはそれを”どの程度”なのかを表現するために，数値で定義し評価できる形にする必要があるのです．
良いADCとは，単にビット数が多ければ良いわけではありません．入力信号をいかに忠実に再現できるかという点が大事になります．その性能を定量的に示す必要があります．
もう一つ重要なのは，理論上の動作だけでなく，実機がどの程度の性能を発揮しているかを数値で把握することです．
設計者は「理論値（理想的なADC）」と「実際のチップ（現実のADC）」を比較し，その差を把握する必要があります．こうした定量的な評価を行うために導入されるのが，SQNR（信号対量子化ノイズ比）と，それに基づくENOB（実効ビット数）です．

SQNR

ここで出てくるのが「信号対量子化ノイズ比（Signal-to-Quantization Noise Ratio）」，

略して SQNR です．名前の通り，SQNRは「信号の大きさ」と「量子化によるノイズの大きさ」の比率を表します．信号のエネルギー（パワー）を \(P_S\)，ノイズのエネルギーを \(P_Q\) とすると，次のように定義されます．

\(\mathrm{SQNR} = \frac{P_S}{P_Q}\)

SQNRが大きいほど，信号の中でノイズが占める割合が小さく，結果として“きれいなデジタル信号”になります．逆にSQNRが小さいと，ノイズが目立ち，信号の忠実度が下がります．

つまり，SQNRは「ADCがどれだけ正確に信号を表現できているか」を測る指標です．

紛らわしいのでまえもって注釈しておきたいのが，「SNR」との違いです．SNR（Signal-to-Noise Ratio）は，通常のアナログ回路などでも使われる指標ですが，量子化によって生じるノイズを明確に区別して考えるために，ADC評価では「SQNR」という表現が使われます．
SNRが総合的なノイズ（回路ノイズやジッタを含む）を指すのに対し，SQNRは量子化ノイズに限定した理論的な値です．

SQNR(正弦波入力)

量子化ノイズを評価する際，入力信号には通常，正弦波が用いられます．

その理由は次の二つです．

1．正弦波は周波数領域で“純粋な1本の線（スパイク）”として現れ，信号とノイズを明確に分けて考えられるため．
2．任意の信号はフーリエ変換によって正弦波の重ね合わせで表現できるため，正弦波を評価信号に選ぶことで他の信号にも一般化できるため．

このとき，理想的なnビットADCのSQNRは次式で表されます．

\(\mathrm{SQNR_{dB}} = 6.02n + 1.76\)

注意しておきたいのが，この式は「正弦波入力の場合」の値です．
(*導出仮定は別途記事にまとめようと思います．)

たとえば，ランプ波を入力とした場合には正弦波よりも約1.76dB低くなります．

\(\mathrm{SQNR_{dB}} = 6.02n\)

これは，同じ振幅範囲でもランプ波の平均パワーが正弦波よりも小さいためです．
つまり，正弦波の方が信号エネルギーが大きく，結果としてより高いSQNRが得られるのです．
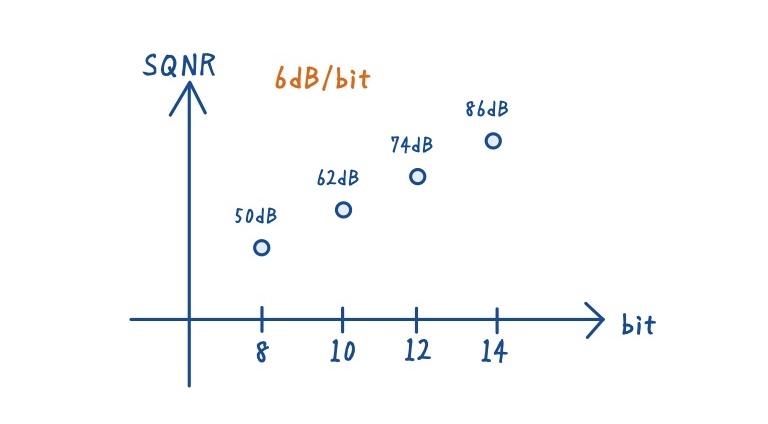
また，この式の中の「6.02」という数字は，ビット数とノイズ低減の関係を直感的に示しています．

1ビット増えるたびに，おおよそ6dB（＝ノイズ電力が1/4）ずつ改善されるという意味です．
この6dB/bitの関係は，ADC設計において非常に実用的な目安として使われます．

実効ビット数（ENOB）という考え方

ここまでのSQNRは，あくまで理想的なADCに基づいた計算結果です．

しかし，実際のADCには回路ノイズやオフセット，ジッタ，スイッチング歪みなど，さまざまな非理想要素が存在します．

そこで，実際のADCの性能を「理論的には何ビット相当か」に換算して表すのがENOB（Effective Number of Bits）です．

\mathrm{ENOB} = \frac{\mathrm{SQNR_{dB}} – 1.76}{6.02}

たとえば，実測でSQNRが60dBだった場合，ENOBは約9.6ビットになります．

“10ビットADCとして設計したが，実際の性能は9.6ビット程度になった．”といったように，ENOBは，実測結果をビット単位に換算して理解できる便利な指標です．

SNR（dB）よりも直感的に理解しやすく，設計上の改善効果を定量的に追いやすいのが特徴です．

周波数領域でSQNRの見える化

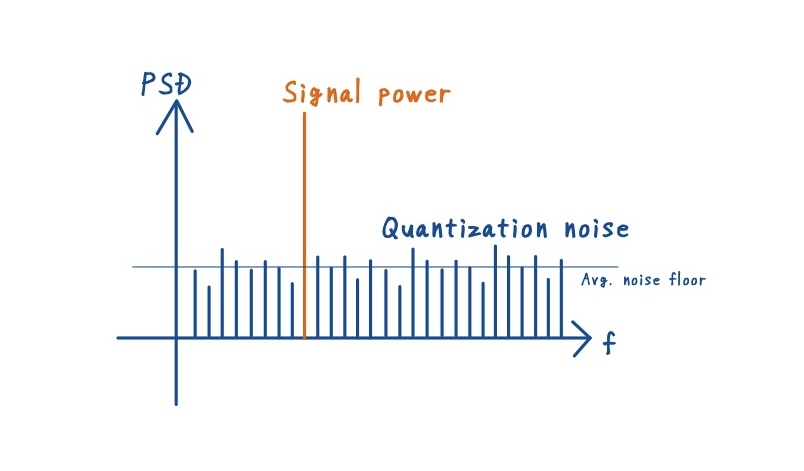
量子化ノイズの影響を評価するとき，時間領域の波形だけを見てもノイズの大きさを定量的に判断するのは難しいです．そこで使うのが周波数領域での解析（FFT解析）です．

時間軸で混ざっていた信号成分とノイズ成分を，周波数軸で分離し，「信号が占めるエネルギー」と「ノイズが占めるエネルギー」を明確に比較します．

講義では，先生が”もしお母さんにお小遣いを頼めないなら，お父さんに頼めばいい”と表現をしていました．ユニークで面白いですね．時間領域で難しいことは，周波数領域に頼ればいいという比喩であり，ADC評価の本質をうまく表しています．

スペクトラムアナライザやFFTベースの解析ツールを用いることで，時間領域では分かりにくいノイズを周波数領域で見える形にすることができるからですね．

まとめ

  • SQNRは信号とノイズの比率を示す基本指標．
  • ビット数が1つ増えるたびに，約6dBずつノイズが低下する．
  • ENOBは実際のADC性能を「ビット数」で表現できる便利な指標．
  • 評価は時間領域よりも周波数領域で行うのが一般的．

以上です．最後まで読んでいただきありがとうございました．

次回は，SQNRの式
\(\mathrm{SQNR_{dB}} = 6.02n + 1.76\)
を一歩ずつ導出していきます．「6.02」と「1.76」という数字がどこから現れるのか，数学的に追いかけて理解していくつもりです．

参考文献

本記事はあくまで筆者の勉強備忘録のため，より正確に理解したい，さらに深く理解したい場合は下記をご参照ください．

今回解説した内容は下記講義動画を参考にしています．

コメント

タイトルとURLをコピーしました