ADC勉強会 -量子化-

はじめに

アナログ信号をデジタルで扱うためには，入力された連続信号を離散化する必要があることを前回までに説明しました．時間軸方向を離散化するサンプリングについて学びましたが，離散化が必要なのは時間軸だけではありません．今回のトピックである量子化は振幅方向，つまり物理量を離散値に変換する操作です．

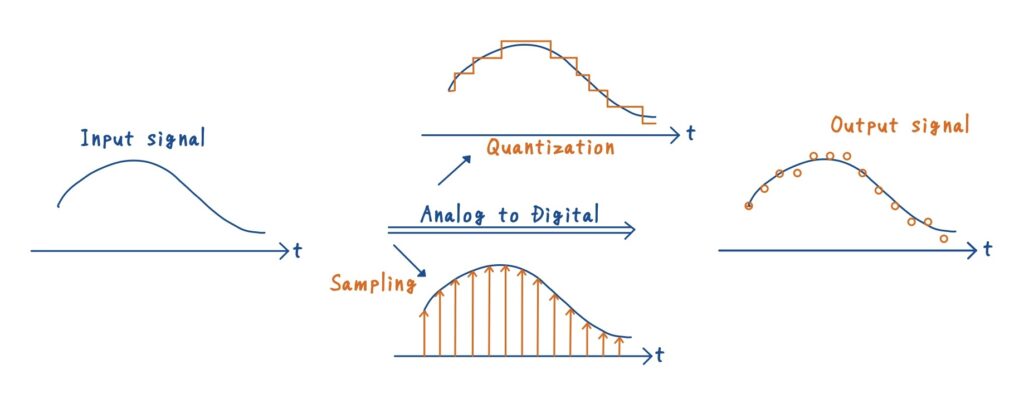
サンプリング（時間方向の離散化）と量子化（振幅方向の離散化）を組み合わせることで，無限の情報を持っていた連続信号を，0と1のみで表現できるデジタル信号に変換することが可能になります．

サンプリングと量子化の順番は理論上どちらでも構いませんが，一般的には実装の容易さからサンプリングを先に行い，その後量子化を行います．

量子化とは「ビット数で表現できる範囲に信号の振幅を落とし込む」操作であり，一見単純に思えますが，実は信号をどれだけ正確に再現できるかを左右する非常に重要な要素です．本記事では，量子化の目的と役割，仕組み，そして誤差の扱い方を整理し，次回取り上げる「SQNR」や「ENOB」といった評価指標への基礎とします．

量子化の目的

量子化の目的は，信号を有限ビットに収め，デジタル処理を可能にすることです．

もしコンピュータに無限の情報を格納・処理する能力があるなら，入力信号をそのまま保存すればよいでしょう．しかし現実のシステムにはメモリや通信路に限界があり，必ずビット数の制約があります．

そこで，信号の振幅を有限の目盛りに丸め込むことでデジタル化を実現します．ここで重要になるのは次の二点です．

・何ビットあれば十分な分解能が得られるのか
・そのとき誤差はどの程度になるのか

量子化は「目盛りを粗くすればデータは軽くなるが誤差は増える，細かくすれば誤差は減るがデータは重くなる」という典型的なトレードオフです．

基本的な定義

量子化は物理量を離散化する操作です．ここでいう物理量とは電気信号を想定しています．ADCでは電圧を対象とすることがほとんどです．

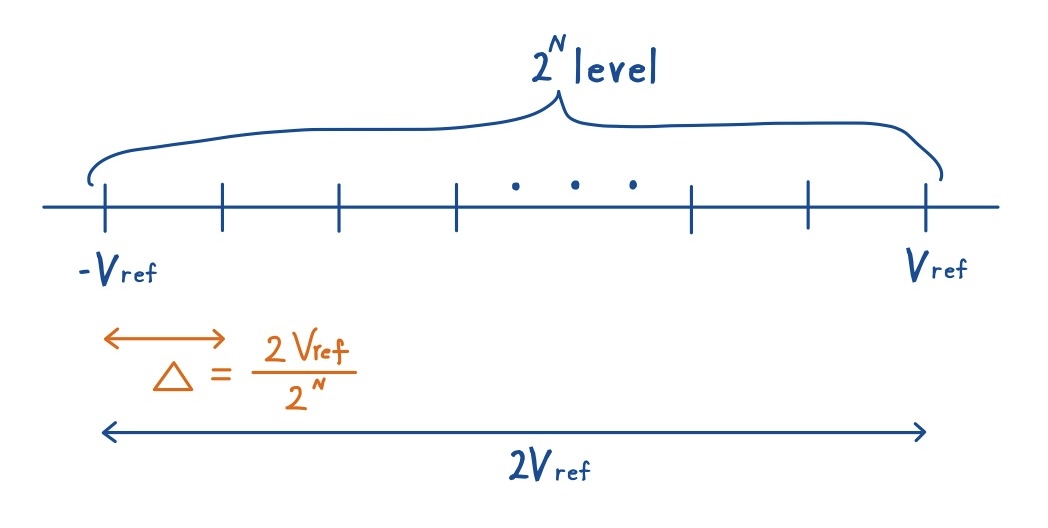
入力信号の範囲をフルスケール（Full Scale Range, FSR）と呼び，以下のように表します．

\([-V_{\text{ref}}, +V_{\text{ref}}]\)

このレンジを有限のレベルへ分割し，その区間に応じて代表値に丸めるのが量子化です．

  • nビットで表現できるレベル数は \(2^n\)
  • ステップ幅（量子化間隔） \(\Delta\) は\(\Delta = \frac{2 V_{\text{ref}}}{2^n}\)

例：3ビットの場合

  • レベル数： \(2^3 = 8\)
  • ステップ幅： \(\Delta = 2V_{\text{ref}}/8\)

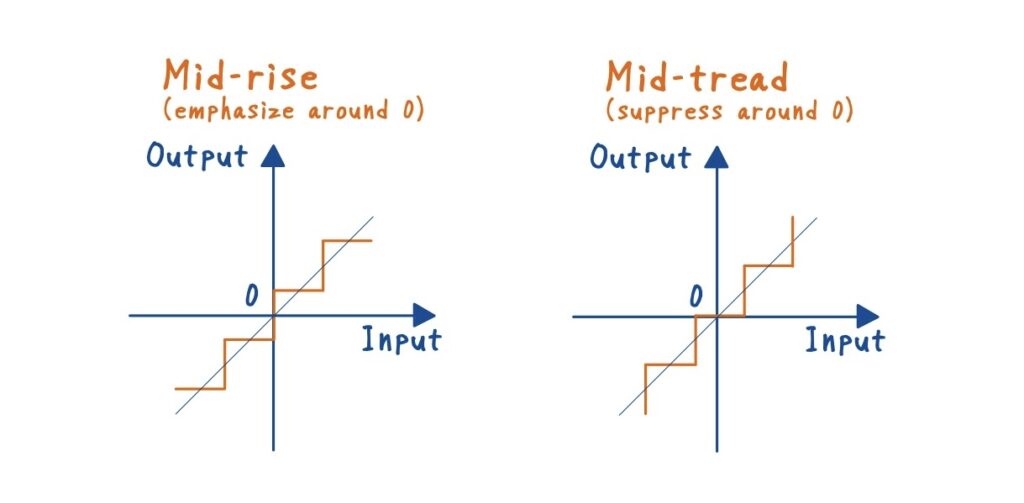
量子化方式：Mid-Riser と Mid-Tread の比較

ADC の基本動作を考えるとき，避けて通れないのが「量子化方式」の違いです．代表的なのは Mid-Riser 型と Mid-Tread 型 の二つです．まずは，それぞれの特徴を整理します．

表

方式メリットデメリット
Mid-rise・量子化誤差が常に一様に分布
・SNR の導出に使われる標準モデル		・ゼロ入力でも非ゼロ出力
・ゼロコードを持たないため，デジタル処理で扱いづらい
Mid-tread・ゼロ入力とゼロ出力が対応
・符号付き処理や DSP との相性が良い
・0レベル付近のノイズを除去		・Mid-rise型より+1bit必要

講義内では，Mid-rise型が主流だと説明がありましたが，これらの2つの方式はどちらも一長一短の特徴があります．そのため，実際の ADC では，アーキテクチャや用途によって採用方式が変わります．

・単極性入力（0〜Vref）→ ゼロをまたぐ必要がないため Mid-rise 型 が自然．
・双極性入力（±Vref）→ ゼロ入力にゼロ出力を対応させたいので Mid-tread 型 が主流

ただし理論モデルとしては偶数レベルで扱いやすいMid-Riser型が主流です．以降の議論でもMid-riseをベースに進めます．

量子化誤差とモデル化

量子化によって，入力信号を有限な値へ丸め込みを行うと，当然ながら誤差が生じる場合があります．この誤差のことを量子化誤差と呼びます．

入力信号をv，量子化後の出力信号をyとすると，入力と出力の差分が量子化誤差qとなり，下式で表されます

\(q = v – y\)

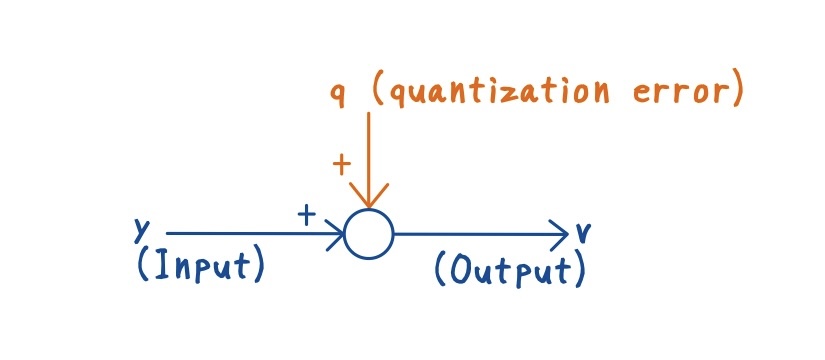
量子化誤差(決定論的な性質)

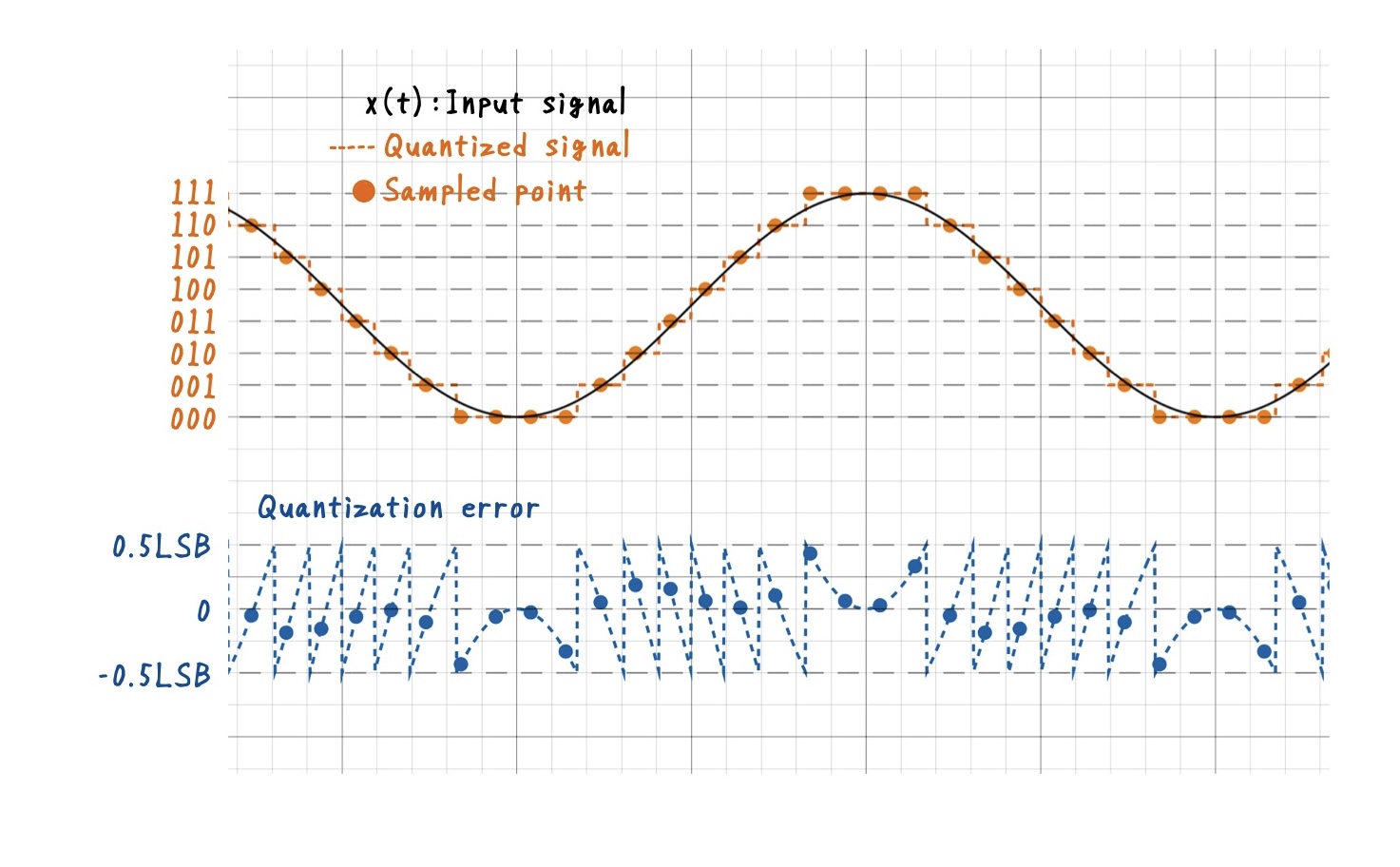
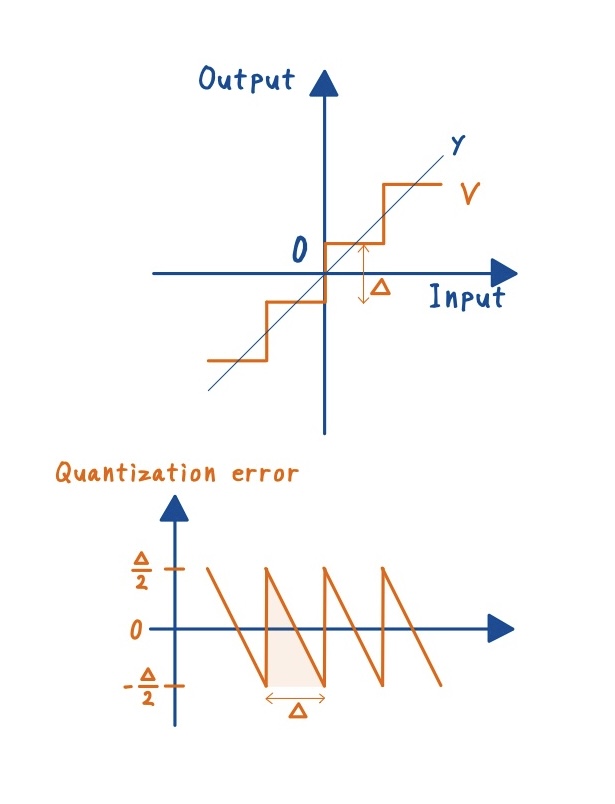
量子化誤差を確認するために，下図に入力値と量子化後の出力値の関係およびその差分を示します．量子化を行うと有限のレベルへ丸め込まれるため，入力値に対して，階段上の出力特性を示すことが分かります．その結果，入力値-出力値は鋸形状になることが分かります．この誤差は，入力がどの区間に入ったかによって決まり，必ず [-Δ/2, +Δ/2] の範囲に収まります．

このことからわかるように，量子化誤差は，入力が与えられれば必ず一意に決まります．つまり，本質的には決定論的な誤差です．しかし，その入出力関係は直線ではなく階段状であり，入力と出力の対応は非線形です．この非線形ということが重要であり，例えば入力値が増減しても，出力は同じレベルに留まり続ける場合があり，比例関係が成り立ちません．

このように量子化誤差は「入力依存で決まるけれど線形でない」という点が，量子化誤差を厳密に扱いにくい理由です．

量子化ノイズ(確率的なモデル化)

量子化誤差は決定論的ということを説明しました．しかし，入力信号が常に既知であるとは限らないため，この誤差を入力に依存して逐一解析するのは実用的ではありません．さらに，階段上の入出力特性は非線形であるため，解析が複雑になります．

そこで，量子化誤差を入力に依存しないランダムな雑音として確率論的なモデル化をします．これを量子化ノイズと呼びます．具体的には以下の仮定を置きます．

1．誤差 Q は入力信号に依存しない（独立性仮定）
2．誤差は範囲 [-Δ/2, +Δ/2] に一様分布する（等確率仮定）
3．サンプル数が十分に多く，すべての離散値が等しい確率で出現する
4．量子化ステップは等間隔である
5．隣接サンプル間の誤差に相関がない

これらの仮定のもとでは，誤差の平均はゼロとなり，分散（＝ノイズ電力）は次式のように導出できます．

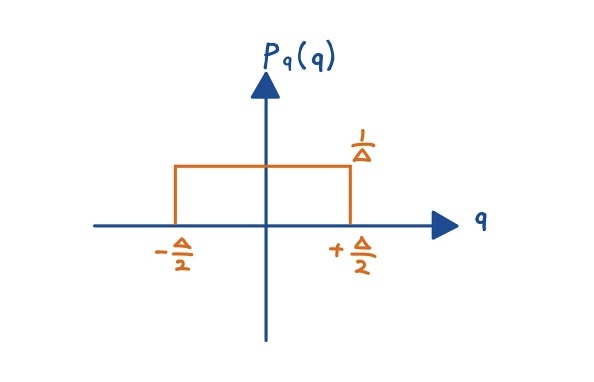
\(p(q) = \begin{cases} \frac{1}{\Delta}, & -\frac{\Delta}{2} \le q \le +\frac{\Delta}{2} \\ 0, & \text{otherwise} \end{cases}\)

このとき、分散は期待値計算で求められます．

\(E[q^2] = \int_{-\Delta/2}^{+\Delta/2} q^2\,p(q)\,dq = \frac{1}{\Delta}\int_{-\Delta/2}^{+\Delta/2} q^2\,dq = \frac{\Delta^2}{12}\)

このように，量子化誤差を確立モデルとして考えることで，誤差の平均値や分散を完結に計算することができ，統計的に扱いやすくなります．また，評価指標である信号対量子化ノイズ比（SQNR）や実効ビット数（ENOB）へと直結します．

まとめ

  • 量子化誤差は，入力依存で決定論的に決まる
  • 非線形な階段特性を持つため，厳密には扱いにくい
  • 実務では「独立・一様分布」の確率モデルで近似し，ノイズとして統計的に評価する
  • この近似により，評価指標（SQNR・ENOB）へと結び付けられる

以上です．最後まで読んでいただきありがとうございました．

今回は量子化について学びました．量子化誤差を考える上で，確立モデルを使う理由が講義を一度聞いただけでは筆者はうまく理解できませんでした．．．確率モデルを扱う意義については，参考文献の『アナログ/デジタル変換入門』を参考にさせていただき，記事の中に説明を盛り込んでいます．”量子化誤差は入力依存で決まるのに，なぜわざわざ入力に依存しないモデルで考えるのか”という点が疑問に思ったのですが，入出力の非線形な関係を考えることで納得しました．

次回は，量子化誤差を定量的に評価する指標である SQNR と ENOB について解説します．

参考文献

本記事はあくまで筆者の勉強備忘録のため，より正確に理解したい，さらに深く理解したい場合は下記をご参照ください．

コメント

タイトルとURLをコピーしました