ADC勉強会 -エイリアシング-

はじめに

前回の記事ではサンプリングの基本式と周波数領域での理解（スペクトルの複製とナイキスト条件）を整理しました．

今回はその続きとして，エイリアシング（aliasing） がなぜ起こるのか，そしてそれを防ぐために不可欠な“アンチエイリアシングフィルタ”（Anti-Aliasing Filter, AAF） について解説します．

エイリアシングとは

サンプリングされた信号のスペクトルは，サンプリング周波数 \(F_s\) ごとに複製されます．

入力信号の帯域幅を \(F_B\) とすると，複製どうしが重ならない条件はナイキストの定理で表されます．

\(F_s > 2F_B\)

もしこの条件を満たさなければ，スペクトルの複製が重なり合い，本来の高周波成分が低周波に化けて現れる現象が起きます．これがエイリアシングです．

数式で確認

高周波の信号がサンプリング後に低周波の信号へ折り返される現象を数式から確認してみましょう．

ここでは，下式のように定義された２つの余弦波について考えます．

  • 低周波余弦波：\(x_1(t) = \cos(2\pi \Delta f t)\)
  • 高周波余弦波：\(x_2(t) = \cos(2\pi(F_s \pm \Delta f)t)\)

サンプリング周波数\(F_s\)に対して，\(\Delta f \)は十分小さい(\(\Delta f \ll F_s\))とし，この2つの信号を\(F_s\)でサンプリングした場合のサンプリング後の信号についてみていきます．なお，\(F_s\)でサンプリングするため，\(x_1 (t)\)に対しては，ナイキスト条件を満たしており，\(x_2 (t)\)に対してはナイキスト条件を満たしておりません．

サンプリング後の2つの信号\(x_1 [n] \)と\(x_2 [n] \)は同じになりました．高域の信号が低域に折り返されることが数式からも分かります．このようにして，「高周波数の正弦波が、サンプリング後には低周波数の正弦波のように見えてしまう」という現象が生じてしまうのです．

さらに，周波数を一般化して \(M \cdot F_s \pm \Delta f \)とした場合も，サンプリング後の信号は同じく \(\Delta f \)にエイリアスします．このことから，「高周波成分が低域に折り返される」というエイリアシングの本質が数式的に確認できます．

時間波形で確認

SSCD Lab の講義では余弦波を例にしていましたが，筆者の方では正弦波でも確認しました．

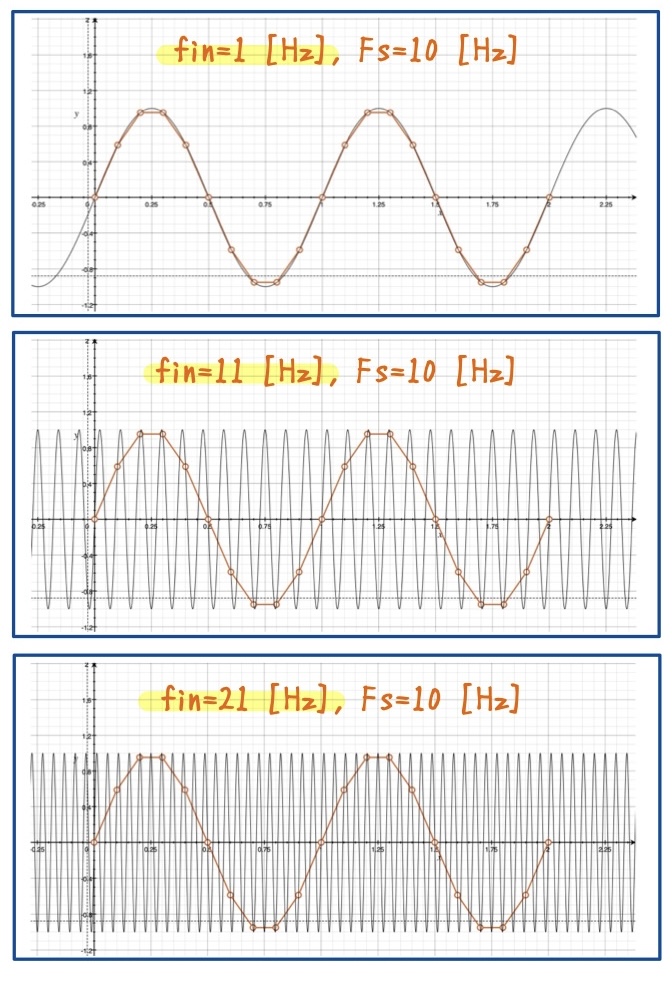
入力周波数 \(f_{in}=1\,\text{Hz}, 11\,\text{Hz}, 21\,\text{Hz} \)をサンプリング周波数 \(f_s=10\,\text{Hz} \)でサンプリングした波形を下図に示します．

  • 黒線：入力信号
  • 橙線：サンプリング後の信号

比較すると，異なる入力周波数であっても，サンプリング後の波形はいずれも同じに見えます．
1 Hz の場合はナイキスト条件を満たしており忠実に再現されていますが，11 Hz や 21 Hz では条件を満たさないため，1 Hz の信号と区別できない形で折り返されてしまいます．
数式での説明と同様に，時間波形からもエイリアシングの直感的理解が得られたと思います．

さらに，折り返し周波数を数式で確認すると，入力周波数とサンプリング周波数の整数倍との差として表せます．
\(\Delta f = |f_{in} – k \cdot F_s|\)

具体的には，
\(\Delta f_in = 21\,\text{Hz} – 2 \cdot F_s = 1\,\text{Hz} \)
\(\Delta f_in = 11\,\text{Hz} – 1 \cdot F_s = 1\,\text{Hz} \)

このように，入力が 11 Hz や 21 Hz であっても，サンプリング後にはいずれも 1 Hz に折り返されます．時間波形の比較と合わせて，「異なる入力周波数が同じ信号として観測される」ことがエイリアシングの本質であると分かります．

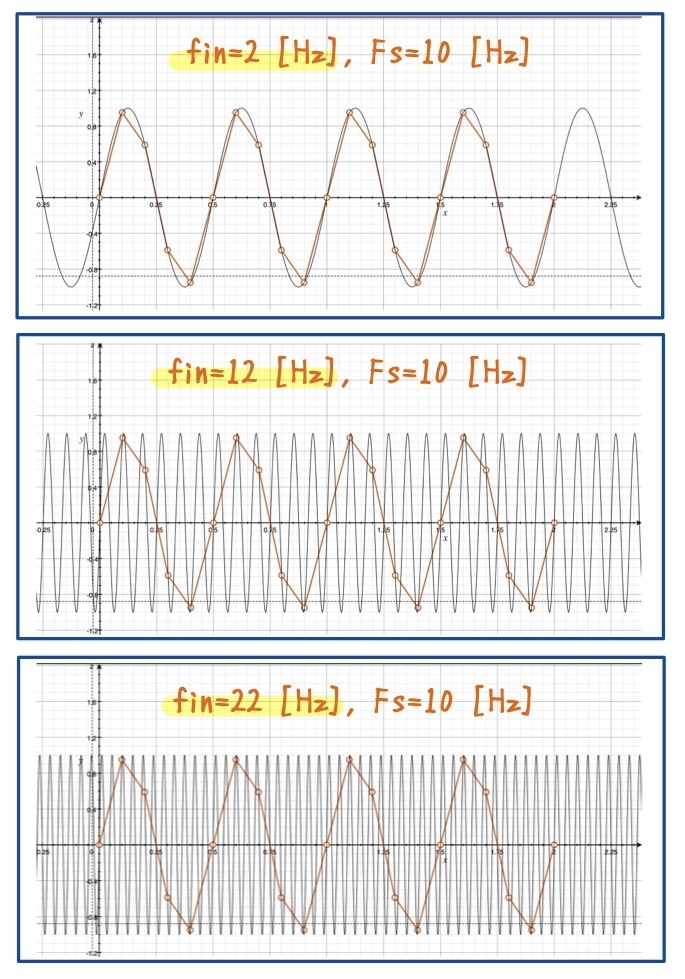
おまけで，\(f_{in}=2\,\text{Hz}, 12\,\text{Hz}, 22\,\text{Hz} \)の波形比較も載せておきます．こちらはMacのGrapherというソフトを使って作成しました．(末尾に付録あり)
こちらも2Hzの時と同様の事象を確認できました．

周波数スペクトルで確認

次に，周波数スペクトルの観点からエイリアシングを見てみましょう．

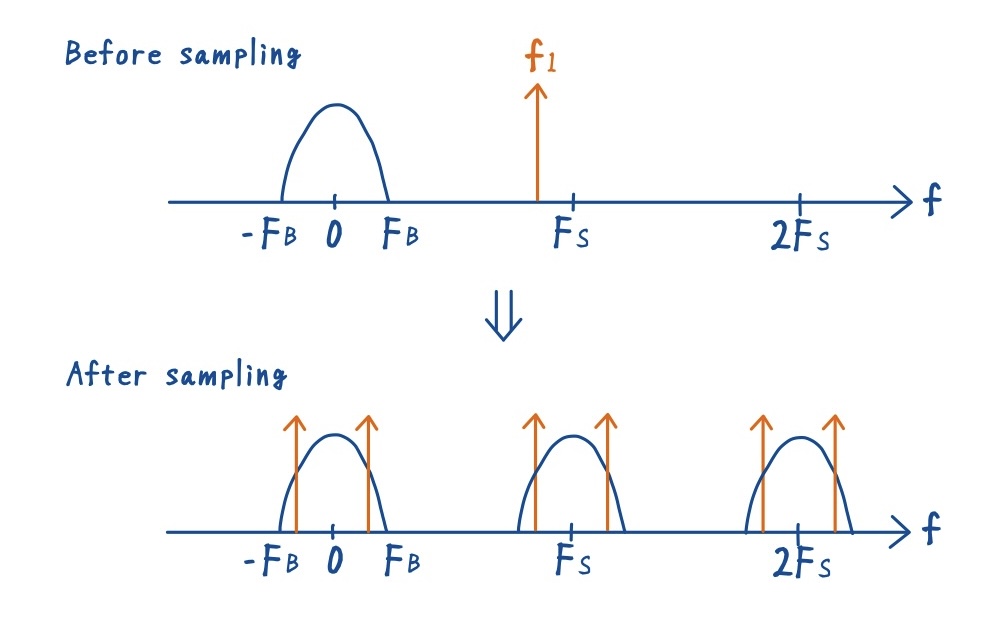
入力信号のスペクトルが帯域 \(F_B\) に収まっていても，現実には帯域外にノイズ成分が存在することがあります．帯域外のノイズ成分が \(f_1\) の周波数である例を用いて考えます．サンプリングを周波数 \(F_s\) で行うと，信号スペクトルは \(F_s\) ごとに周期的に複製され，帯域外の \(f_1\) も折り返されて \(|f_1 – kF_s|\) の形で帯域内に現れます．

図で考えると，\([-F_B, +F_B]\) に収まる信号に対し，外側にあったノイズピーク \(f_1\) がサンプリング後には折り返されて帯域内に入り込み，周期的に繰り返されるように見えます．その結果，サンプリング前には分離していたノイズスペクトルが重なり，本来の信号に干渉して波形を歪めてしまいます．

つまりエイリアシングとは，「帯域外の成分が折り返されて帯域内に重なり，信号スペクトルを変形させる現象」であることが分かります．

直感的な理解（例）

エイリアシングは実世界でもよく観察されます．その例を講義内では下記2つを取り上げていました．

  • ヘリコプターのローターが止まって見える撮影
    →フレームレートとローター回転数が一致すると，静止しているように見える．
  • 水滴が逆流する映像
    →右ストロボ光と水滴落下速度が同期すると，下向きの運動が上向きに見える．

これらはいずれも「サンプリング周波数と実信号の周期性が噛み合って，別の低周波に見えてしまう」典型的なエイリアシング現象です．

その他にも身近な例として次のようなものも挙げられます．

  • LED照明を撮影したときのちらつき（フリッカー）　
    →照明の点滅周波数とスマホの撮影フレームが干渉し，画面上で縞模様や明滅としてエイリアシングが現れる．
  • ディスプレイ撮影時に出るモアレ模様
    →ディスプレイの走査周波数とカメラのサンプリング周期がずれることで，本来存在しない縞模様が生じる．

これらの例からも分かるように、エイリアシングは単なる抽象的な現象ではなく、私たちが日常でよく目にする「見え方の錯覚」として体験できる現象です。

実務上の問題：ノイズの折り返し

先ほど説明したように，理想的なケースでは入力信号は帯域\(F_B\) に収まっていてほしいですが，実際にはそうはいきません．実際の計測系や音響系では，広い周波数範囲にわたってノイズが存在します．環境起因や前段アナログ回路の熱雑音など，いわゆる“ほぼ白色”に近いノイズが上流に広がっているイメージです．

この状態でサンプリング周波数 \(F_s\) でサンプリングすると，信号スペクトルだけでなくノイズスペクトルも \(F_s\) 周期で複製されます．その結果，帯域外の広帯域ノイズが折り返されて \([-F_B,+F_B]\) に重なり込み，帯域内のノイズ床が底上げされます．サンプリング前は信号帯域と分離していたノイズが，サンプリング後には重畳してしまい，信号がノイズに埋もれてしまうことがあります．

これが「エイリアシングが実務上深刻になる理由」です．

アンチエイリアシングフィルタの必要性

ここまでで，エイリアシングの概要と，実世界では必ず帯域外にノイズが存在することを確認しました．この高域ノイズによるエイリアシングを防ぐためには，不要な高周波成分をサンプリング前に除去することが不可欠です．

そこで用いられるのがフィルタです．例えば信号帯域が \([-F_B, +F_B]\) にある場合，その帯域のみを通過させたいのでローパスフィルタを使います．ローパスフィルタとは，その名の通り低周波成分を通過させ（low-pass），高周波成分を遮断するフィルタです．これをサンプリング回路の前段に挿入することで，所望帯域の信号だけを通過させ，それ以上の周波数成分を抑圧できます．

このように，サンプリング前段で不要な帯域外信号を除去する役割を担うフィルタをアンチエイリアシングフィルタ（Anti-Aliasing Filter, AAF）と呼びます．

なお，ローパスフィルタは信号帯域の中心が 0 付近にある場合に適用しますが，もし信号が中周波や高周波を中心とする帯域に存在する場合には，バンドパスフィルタをアンチエイリアシングフィルタとして用います．

役割

  • サンプリング前に不要な高域成分を削る
  • 信号帯域 \([-F_B, +F_B]\) は素通し（Passband）
  • 折り返して侵入する可能性がある帯域 \([F_s-B, F_s+B]\) を十分に減衰（Stopband）

フィルタ設計の観点

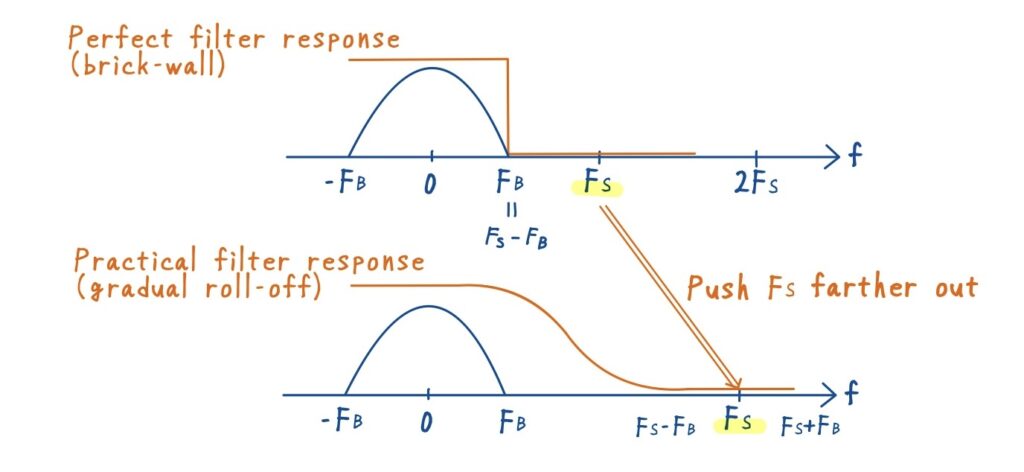
理想的には，下図の上段のように鋭いカットオフ特性を持つフィルタが望ましいです．例えばサンプリング周波数がナイキスト条件ぎりぎりの \(F_s = 2B\) の場合，\([-F_B, +F_B]\) の信号帯域だけを完全に通過させ，それ以外の周波数成分をゼロにすることができれば，余分な成分が折り返される心配はありません．

しかし，このようなフィルタは現実には実現できません．実際のローパスフィルタ（LPF）の特性は図に示すように，高域に向かって徐々に減衰していく「ロールオフ」を持っています．つまり，理想のように通過帯域と阻止帯域を鋭く分けることは不可能で，必ず遷移帯域（transition band）が生じてしまいます．

そのため，実務では設計を現実的にする工夫が必要です．ナイキスト条件 \(F_s > 2B\) を満たすだけでなく，さらに余裕を持ってサンプリング周波数 \(F_s\) を高く設定します．これによって，信号帯域 \([-F_B, +F_B]\) と折り返し成分が侵入する帯域 \([F_s – F_B,\, F_s + F_B]\) の間にガードバンドが生まれます．ガードバンドが広がることで，フィルタの遷移帯域を十分に確保でき，緩やかな減衰特性を持つ現実的なフィルタでも必要な性能を満たせるようになります．

言い換えれば，「理想的な鋭いフィルタを作ろうとする」のではなく，「サンプリング周波数に余裕を持たせて，現実的なフィルタで設計できる環境をつくる」のが実務的なアプローチです．

オーバーサンプリング比（OSR）

実際に使われるサンプリング周波数 \(F_s\) を，ナイキスト周波数 \(2F_B\) で割った値を オーバーサンプリング比（OSR） と呼びます．

\(\text{OSR} = \frac{F_s}{2B}\)

講義内ではOSRについて下記水準が紹介されていました．

  • OSR = 1 → ナイキスト条件ぎりぎり（設計が厳しい）
  • OSR = 2〜4 → 実務でよく選ばれる（フィルタが設計しやすい）

まとめ

  • エイリアシングは「サンプリング周波数より高い成分が折り返して見える現象」．
  • 実機では環境ノイズや回路ノイズが原因で必ず起こるリスクがある．
  • アンチエイリアシングフィルタを前段に挿入し，周波数帯域外の成分を除去することが必須．
  • 実務では オーバーサンプリングによりフィルタ設計を現実的にする．

以上です．最後まで読んでいただきありがとうございました．
もうしばらく理論的な内容が続きますがお付き合いください．

参考文献

本記事はあくまで筆者の勉強備忘録のため，より正確に理解したい，さらに深く理解したい場合は下記をご参照ください．

付録 : Mac標準ソフト Grapher

サンプリングの説明に用いた時間波形はMacの標準ソフトGrapherを使って作図しました．こちらはさまざまなグラフが書けるのでとても便利です．しかし，なかなか使いこなしている人は見当たらず，日本語で解説されている文献は少ない印象です．こちらは標準ソフトながらポテンシャルが高いので，応用先が広そうです．

今回は以下のような設定をしました．
\(f_in\)や\(f_s\)を変えることで，任意の波形を表示させています．

Screenshot

コメント

タイトルとURLをコピーしました