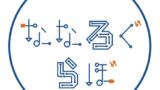ADC勉強会 -サンプリング-

今回からADCの基礎についてまとめていきます．
ADCはその名の通り”Analog-to-Digital Converter”であり，アナログ回路だけでなく情報処理の基礎知識を理解しておく必要があります．そのため，しばらく理論的な内容が続きます．

今回はまずADCの大きな概要と，サンプリング(標本化)についてです．

ADCとは

身の回りに存在する——音声、温度、光、力、映像——はすべてアナログな情報です．一方で，コンピュータやスマートフォン，通信システムが処理できるのはデジタルな情報だけです．この「アナログ」と「デジタル」の世界をつなぐ役割を果たすのが ADC（Analog-to-Digital Converter：アナログ‐デジタル変換器）です．

デジタルな情報とはつまり，0と1の組み合わせで表現できる情報です．
ブロック図にADCとDSP(Digital Signal Processing<ディジタル信号処理>) の関係を示すといかのようになります．
ADCへ入力される信号は時間的に途切れなく続く「連続信号」ですが，コンピュータは無限に続く情報をそのまま扱うことはできません．そのため信号を離散化し，後段のDSPで扱える状態に加工してあげる(情報を間引く)必要があります．そうすることで，後段のDSPではフィルタリングやフーリエ解析など，さまざまな処理が可能になるわけです．つまり，ADCは単なる変換器ではなく，計測や制御，通信のすべての出発点になります．

簡単に言ってしまえば，この「情報の間引き具合」がADCの性能を決めるイメージです．(ただし，間引きすぎては当然ダメですし，逆に間引かなすぎても効率や実現可能性の点で問題が生じます．必要アプリケーションや仕様に応じて，適切な精度に落としこむことがADCの設計するやりがいです．)

本記事では，その最初のステップであるサンプリング(標本化)を，時間領域と周波数領域の両面から整理します．

サンプリング(標本化)とは

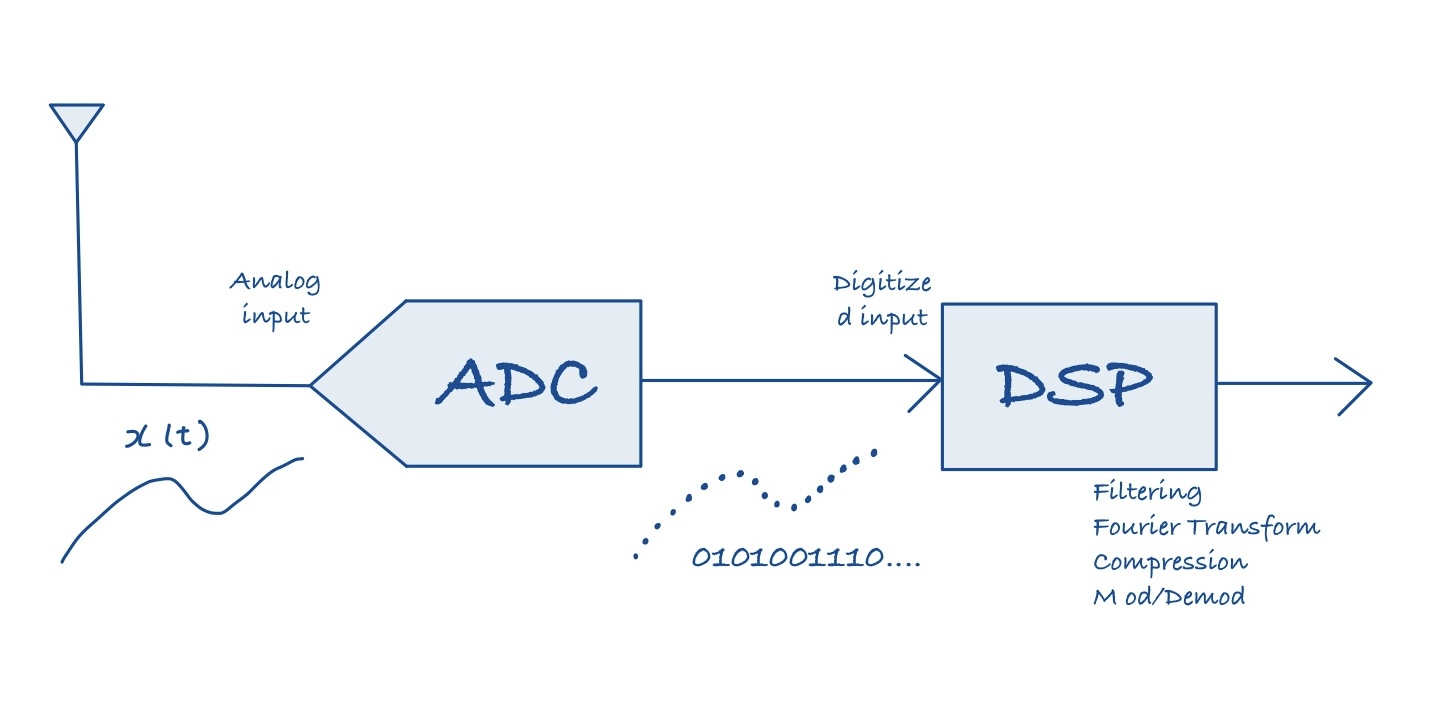
サンプリングとは，時間軸を一定間隔ごとに区切って信号を取り出すことです．(離散化)
先ほど書いたように，アナログ入力信号は連続な信号です．離散化とは，この連続な信号を一定の間隔\(T_s\)ごとに取り出す処理です．時間軸に目盛りを打つため，例えるならば「コマ撮り」のイメージです．このコマ撮りをすることによって，入力された連続時間信号を離散時間信号にすることができます．この処理をサンプリングと呼びます．

\(x[n] = x(nT_s) \quad (n = 0, \pm 1, \pm 2, \dots)\)

この数列 \(x[n]\) が「離散時間信号」であり，入力信号\(x(t)\)の時刻が\(T_s\)の整数倍のときの値を拾っています．この値を拾う時間間隔\(T_s\)の逆数を\(F_s\)とし，サンプリング周波数と呼びます．

\(F_s = \frac{1}{T_s}\)

数学モデル：インパルス列による表現

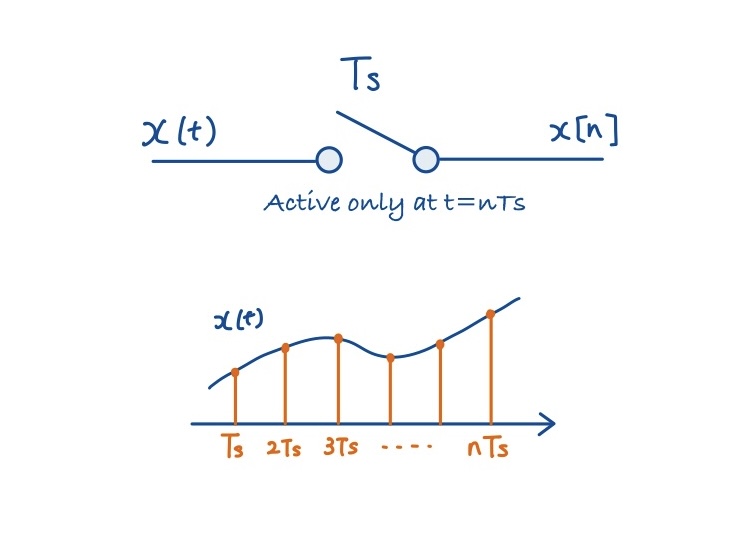
連続時間信号を離散化する操作は、「信号に周期的なインパルス列を掛け算する」と考えることができます．周期インパルス列はデルタ関数を用いて

\(p(t) = \sum_{n=-\infty}^{\infty} \delta(t-nT_s)\)

と表されます．これを入力信号 \(x(t)\) に掛け合わせると，

\(x_\delta(t) = x(t) \cdot p(t) = \sum_{n=-\infty}^{\infty} x(nT_s)\,\delta(t-nT_s)\)
となります．下図にその概略をブロック図で示しました．この式は「サンプリング値 \(x(nT_s)\) を重みとするデルタ関数列」です。これを「離散信号」と見なして定義するのがサンプリングの数式モデルです。

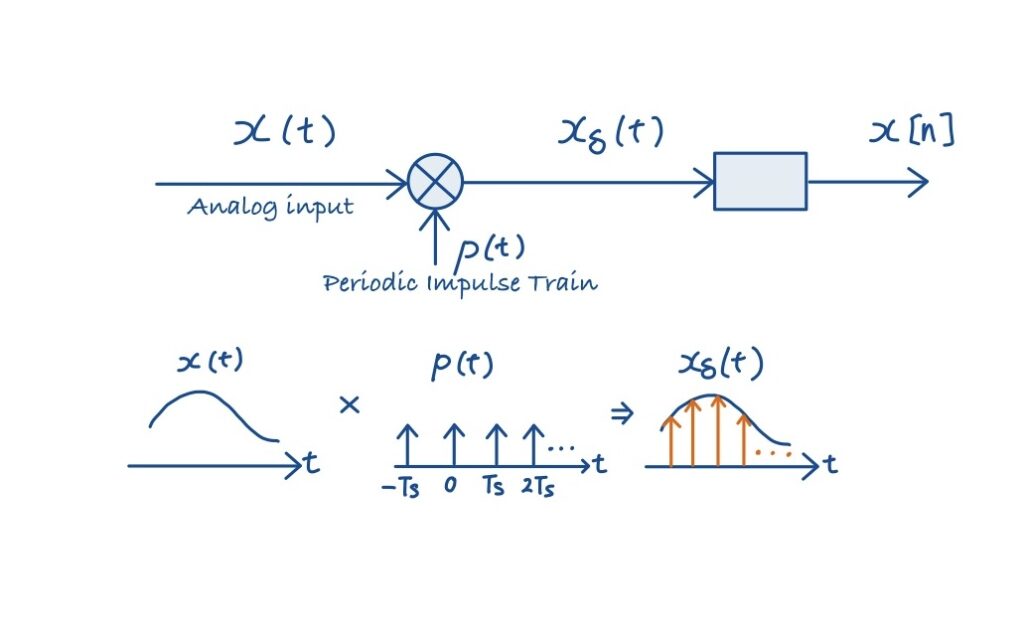
注意すべき点は，\(x_{\delta} (t)\)は依然として連続信号であることです．これはデルタ関数が時刻\(t=nT_s\)以外では0という値になるためであり，最終的な離散時間信号は”離散インデックス付きのデルタ列”の形\(x[n]\)にしてあげることで，初めてデジタル信号として扱えるようになります．．

フーリエ変換

さて，ここまでで時間軸を細切りにして，連続時間信号を離散時間信号へ変換するイメージが掴めたと思います．時間軸でのコマ撮りイメージに加えて、サンプリングの本質を理解するには周波数領域で考える方が直感的です．例えば今後登場するエイリアシング/アンチエイリアスフィルタ/SNR等の現象がその代表例ですが，それらは周波数軸に移すことで理解が進むはずです．また，システムとしても周波数信号を処理する方が圧倒的に効率的で設計しやすいです．

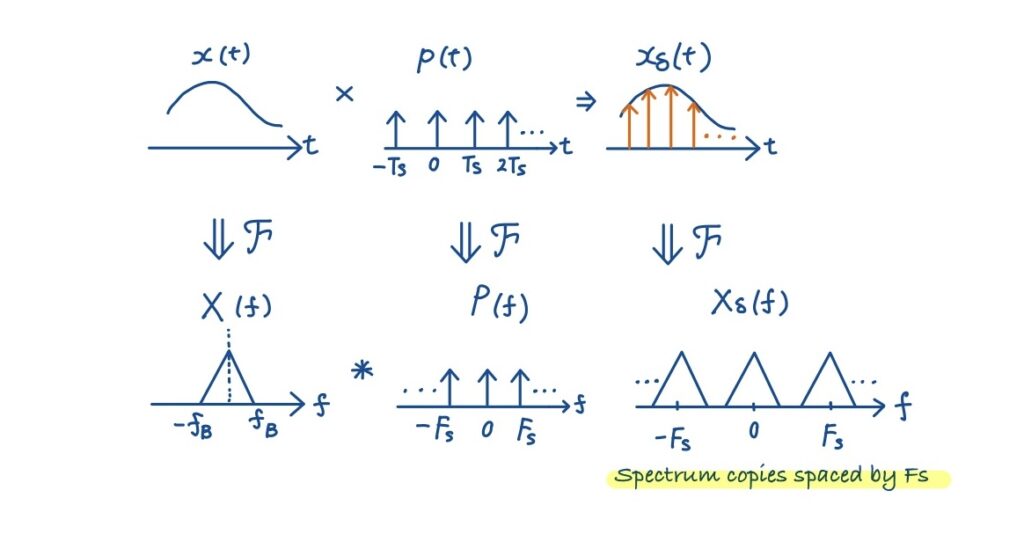
では，順番に説明していきます．先ほど説明した時間信号 \(x(t)\) とデルタ関数 \(p(t)\) の掛け算をフーリエ変換を用いて周波数領域へと変換します．ここで，重要なのは時間領域での掛け算は周波数領域での畳み込みに対応します．(コンピュータで周波数信号が扱いやすい理由の一つです．)

\(X_s(f) = X(f) * P(f)\)

ここで，周期インパルス列のフーリエ変換は

\(P(f) = \frac{1}{T_s} \sum_{k=-\infty}^{\infty} \delta(f-kF_s)\)

なので，入力信号\(x(t)\)とインパルス列\(p(t)\)のフーリエ変換は下記で表されます．

\(X_s(f) = \frac{1}{T_s} \sum_{k=-\infty}^{\infty} X(f-kF_s)\)

上式を見て分かるように，元の信号のスペクトル\(X(f)\)が周波数軸上で\(F_s\)間隔で複製されるようになります．この「スペクトルの複製」が，サンプリングを理解する上で最も重要なポイントです．

離散時間フーリエ変換(DTFT)

厳密に言えば，これまで説明してきたものは「連続時間信号のフーリエ変換」でした．しかし実際にサンプリングで得られるのは 数列 \(x[n]\) です．したがって、処理対象は「離散時間信号」であり，用いる変換はフーリエ変換ではなく 離散時間フーリエ変換（DTFT） になります．

連続 → 離散になったことで，変換式の形も 積分 → 総和 に変わる点が重要です．

\(x[n] = x(nT_s)\)

数列\(x[n]\)に対する離散時間フーリエ変換(DTFT)の定義は次のとおりです．

\(X_d(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}\)

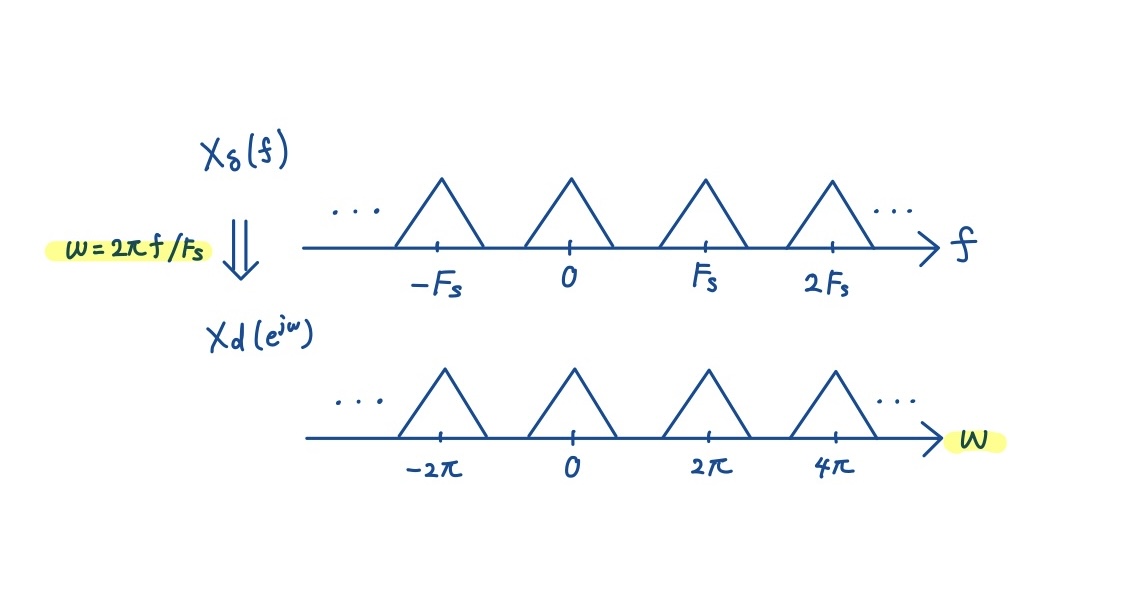
ここで，連続時間周波数 \(f\) と離散時間周波数 \(\omega\) は次のように対応します．

\(\omega = 2\pi f T_s = \frac{2\pi f}{F_s}\)

  • \(f=0 \Rightarrow \omega=0\)
  • \(f=F_s/2 \Rightarrow \omega=\pi\)
  • \(f=F_s \Rightarrow \omega=2\pi\)（周期の境界に対応）

したがって，DTFTのスペクトルは \(2\pi\) 周期で繰り返されることがわかります．

ここまでは定義の話にとどめます．より詳しく理解したい場合は，参考文献をご参照ください．(フーリエ変換まわりの話はどこかでシステムとの対応を交えて記事化したいと思います．)

ナイキスト条件

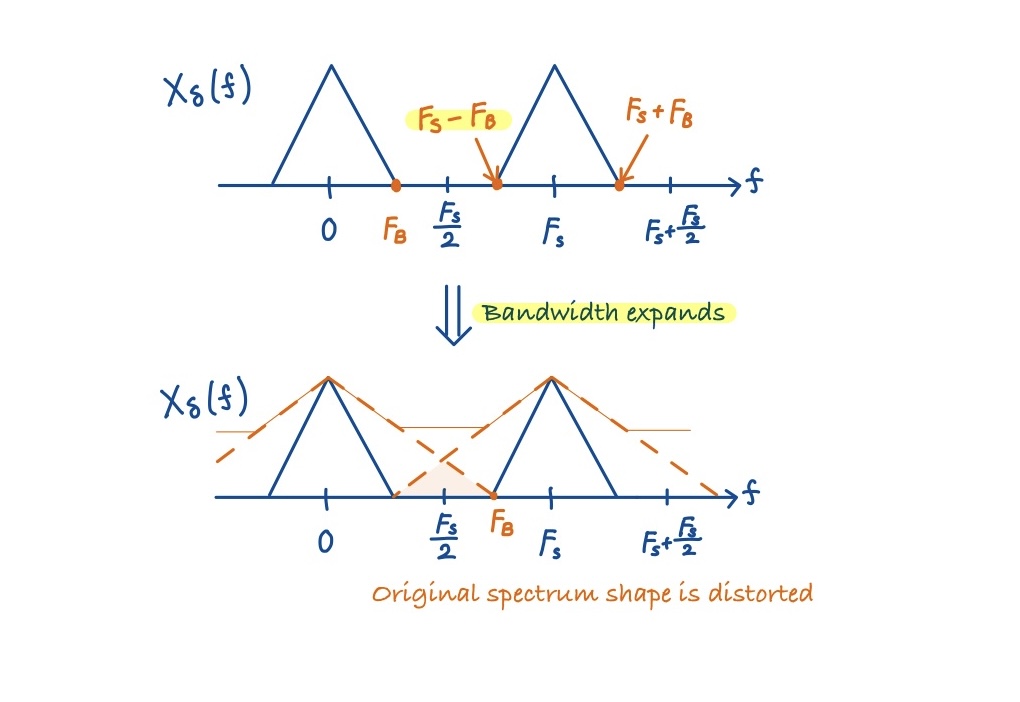
サンプリングをすることで，元の信号スペクトルが周波数軸上で\(F_s\)の周期で繰り返されることがわかりました．今，周波数スペクトルを三角形△で示していますが，このスペクトルの裾が広がっていったらどうなるでしょうか．やがて，繰り返されている隣のスペクトルと重なってしまいますね．スペクトルが重なってしまうと，エイリアシングが発生してしまいます．(次回説明予定) 直感的には，隣り合うスペクトルが重なってしまうと，元の信号のスペクトルの形が崩れてしまう→元の信号を復元できない．と考えてください．

では，どうすれば良いか．周波数スペクトルの帯域\(F_B\)が\(F_s – F_B\)に重ならなければよいのです．つまり\( F_B < F_s – F_B\)．ここから，ナイキストの周波数条件\(F_s > 2F_B\)が説明できます．

つまり，観測したい信号の帯域\(F_B\)に対して，その倍以上の周波数でサンプリングしなければ元の信号を復元できない，といった意味になります．

例えば，人間の可聴域の上限である 22kHz の信号をサンプリングする場合，サンプリング周波数は少なくとも 44kHz より高くする必要があります（実際のCD規格では 44.1kHz が採用されています）．

*もっと直感的に理解したい場合は”ナイキスト周波数” あるいは”ナイキスト条件”などで検索してみてください．アニメーションで分かりやすく説明しているサイトがたくさんあります．

まとめ

  • サンプリングとは，連続時間信号を離散時間信号へコマ撮りにすること
  • サンプリングは時間領域では「信号×インパルス列」，周波数領域では「スペクトルの複製」として理解できる．
  • ナイキスト条件 \(F_s > 2F_B\) を満たさないと，エイリアシングが発生し元の信号を復元できない．

以上，最後まで読んでいただきありがとうございました．

今回はLecture 1の冒頭~20分くらいまで進んだかと思います．
また，ディジタル信号処理は下記サイトが個人的に最も丁寧に解説されていると思います．
(これまで何度もお世話になったサイトです)

やる夫で学ぶディジタル信号処理


次回，エイリアシングとアンチエイリアスフィルタについて備忘録を残していこうと思います．

参考文献

本記事はあくまで筆者の勉強備忘録のため，より正確に理解したい，さらに深く理解したい場合は下記をご参照ください．

コメント

タイトルとURLをコピーしました